¿Qué significa para los estudiantes si están aprendiendo que la tecnología puede responder a todos los desafíos?
Las computadoras han ayudado a acelerar la investigación matemática en múltiples direcciones y han aumentado la presencia de las matemáticas en la vida cotidiana.
El papel de la tecnología en la enseñanza y el aprendizaje de las matemáticas está cada vez más presente en mi mente como instructor de matemáticas que ve la llegada de nuevos estudiantes a la Universidad Simon Fraser (SFU) cada año. Ambos en SFU, y cuando visito las aulas de matemáticas canadienses como oradora invitada, Miro a las habitaciones llenas de jóvenes vibrantes rodeados de calculadoras, computadoras y teléfonos inteligentes.
Y eso está bien. Como muchos matemáticos, No me he opuesto a los nuevos vientos tecnológicos propiciados por los tiempos modernos. Pero dicha tecnología debería mejorar y ampliar, en lugar de reemplazar, la capacidad de pensar matemáticamente.
¿Adiós a la geometría?
Recientemente, Conocí a una persona joven que estaba interesada en matemáticas y computación, pero no estoy seguro de en qué dirección le gustaría ir. Ofrecí el siguiente problema utilizado por la Universidad de Oxford para entrevistar a candidatos de licenciatura en matemáticas:"Imagínese una escalera apoyada contra una pared vertical con los pies en el suelo. El peldaño medio de la la escalera se ha pintado de un color diferente en el lateral, para que podamos verlo cuando miremos la escalera de lado. ¿Qué forma traza ese peldaño del medio cuando la escalera cae al suelo? "
Una forma de abordar el rompecabezas de la escalera es usar, de una manera relativamente simple, Geometría euclidiana, para mostrar que la respuesta es un cuarto de círculo. Vea abajo:
En lugar de basarse en propiedades geométricas, el joven usó el lenguaje de programación Python para animar el problema y encontrar la forma requerida. Había aprendido Python por su cuenta a principios de ese verano. Cuando le pregunté sobre triángulos congruentes, el joven parecía perplejo.
Situaciones como esta me hacen temer que si no se usan con el debido cuidado en las aulas, la tecnología puede privar a los estudiantes de desarrollar plenamente sus habilidades numéricas y espaciales.
Problemas inalcanzables
Lo que los matemáticos llaman "el enfoque asistido por computación" ha permitido a los investigadores explorar y resolver problemas matemáticos que de otro modo serían inalcanzables. Me viene a la mente la demostración asistida por computadora del célebre Teorema de los Cuatro Colores.
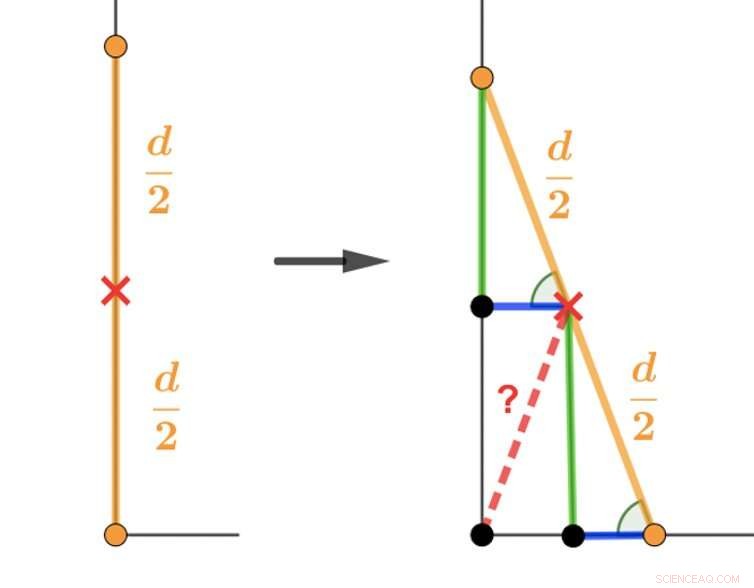
La geometría euclidiana se puede utilizar para resolver el problema que se les presenta a los candidatos de licenciatura en matemáticas de la Universidad de Oxford. Crédito:Veselin, Autor proporcionado
Pero algunas preguntas matemáticas han demostrado las limitaciones de la tecnología existente, y el hecho de que algunas soluciones dependen en gran medida de la intuición humana, inspiración e inteligencia. Uno de esos problemas conocido como el problema de la fiesta (sí, como en una cena), es encontrar el número de invitados que garantizaría que siempre se pueden encontrar seis personas que son amigos en común o seis personas que son extraños en común.
En términos matemáticos, este problema consiste en encontrar lo que se llama "el número de Ramsey R (6, 6), "relacionado con una rama de las matemáticas que estudia qué condiciones deben existir para que aparezca un patrón dado.
Por extraño que parezca, desde 1930 los matemáticos saben que R (6, 6) existe; desde 1994 sabemos que este número está entre 102 y 165.
¡Ningún progreso desde entonces!
Matemáticas experimentales
Los célebres matemáticos y hermanos canadienses Peter Borwein y Jonathan Borwein, que establecieron el Centro de Matemáticas Experimentales y Constructivas en 1993 en SFU, estuvieron entre los pioneros de la investigación que contribuyeron al proceso de alinear las matemáticas y las nuevas tecnologías.
Como sugirieron Jonathan Borwein y el matemático David H. Bailey, Las matemáticas experimentales utilizan "un enfoque asistido por computación para la investigación matemática". Querían decir que la matemática experimental consiste en usar computadoras para impulsar procesos que han sido los elementos básicos de la investigación matemática durante siglos:
También argumentaron que las computadoras podrían ayudar a realizar largas derivaciones matemáticas y confirmar los resultados obtenidos analíticamente.
Su punto era que las computadoras permiten a los investigadores llevar sus exploraciones a dimensiones nuevas o diferentes.
Nueva exploración
Las ideas de Bailey y Borwein pueden usarse para ayudar a describir formas contemporáneas y futuras de enseñar matemáticas para ayudar a los estudiantes a ver los problemas de nuevas formas.
En mi anécdota de geometría-Python, Podría haber desafiado al estudiante al observar que la forma obtenida por la animación generada por Python solo parece un cuarto de círculo (esto puede referirse a los puntos 1-3 y 5 en la definición de Bailey-Borwein) y que una respuesta completa requeriría una resultado derivado analíticamente (punto 6).
Para justificar el desafío, También podría optar por mostrarle al estudiante una prueba visual aparentemente alucinante, como la animación que "muestra" 64 =65.
Podría concluir citando al matemático y filósofo del siglo XVII René Descartes, quien resolvió:"... nunca aceptar como verdadero nada que yo no supiera claramente que era tal; es decir, con cuidado ... evite ... los prejuicios, y no comprender nada más en mi juicio que lo que se me presentó a la mente de manera tan clara y distintiva como para excluir todo motivo de duda ".
Currículos de matemáticas experimentales
Los investigadores y educadores han desarrollado planes de estudio que se especializan en enseñar a los niños y jóvenes cómo usar las computadoras para mejorar y extender su propio aprendizaje y pensamiento matemático en las escuelas secundarias canadienses. Por ejemplo, El Proyecto Curricular de RabbitMath, dirigido por el matemático Peter Taylor de Queen's University y Chris Suurtamm de la Universidad de Ottawa, o el Proyecto Callysto, promovido por el Instituto Pacífico de Ciencias Matemáticas (PIMS) y la organización sin fines de lucro Cybera, con sede en Alberta.
El desafío para la comunidad docente de matemáticas consistirá en crear y mantener cada vez más un equilibrio saludable en nuestras aulas entre el poder del rigor, matemáticas formales y el poder de la computación.
Cuando pienso en el futuro Me preocupa que las partes rigurosas y formales de las matemáticas puedan desaparecer y quedar fuera del alcance de los estudiantes.
Para un estudiante en un futuro no muy lejano, haría, por ejemplo, el número pi se convierte en un número racional, es decir, ¿Sería igual a su aproximación generada por la computadora más poderosa en este momento?
Más importante, ¿Qué significará todo esto para los estudiantes y su aprendizaje de las matemáticas como instrumento para navegar mejor por el mundo que los rodea?
Este artículo se vuelve a publicar de The Conversation con una licencia de Creative Commons. Lea el artículo original. 