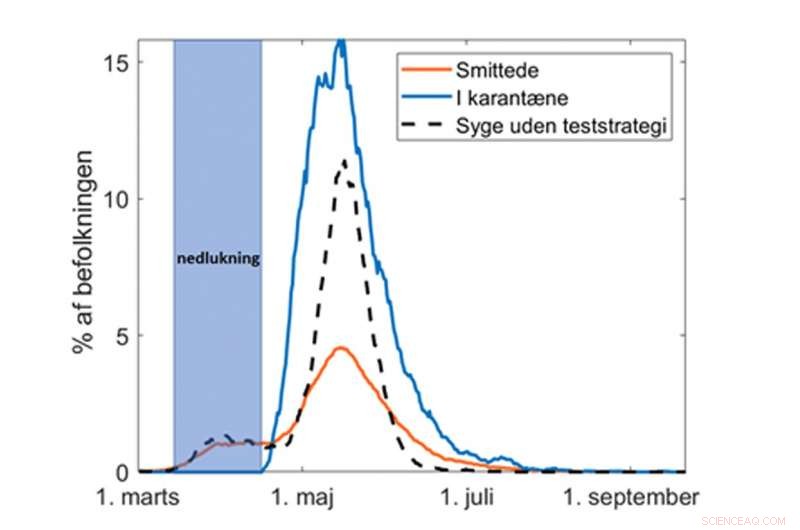
Figura 1:Comparación entre dos escenarios:con bloqueo, prueba y rastreo de contactos y sin prueba y rastreo de contactos. La línea naranja muestra el número de personas enfermas en el escenario con seguimiento de contactos, y la línea azul muestra el número de personas en cuarentena. La línea punteada muestra el número de personas enfermas en el escenario sin rastrear la infección. El eje X es el% de la población danesa. Crédito:Instituto Niels Bohr
COVID-19 está impactando actualmente a todo el mundo y se están probando diferentes enfoques para detener la epidemia en todo el mundo. A medida que pasan las semanas aprendemos cada vez más sobre este pequeño virus, que afecta tanto a nuestra vida cotidiana y a nuestro mundo. En la sección de biocomplejidad del Instituto Niels Bohr (NBI), Universidad de Copenhague, los investigadores están ocupados aplicando métodos de la física de sistemas complejos para examinar cómo se maneja mejor la epidemia. Los, por ahora, La forma más sencilla y conocida es el "bloqueo, "que hemos estado atravesando durante los meses de marzo y abril. También es el más caro, demostró ser eficiente, algo que no podíamos saber antes de probarlo. Pero hay muchas formas de calcular y pronosticar el desarrollo de la epidemia, y los investigadores en biocomplejidad y sistemas complejos explican uno de ellos aquí, así como algunos de los conceptos más prevalentes presentados en los medios.
Modelos matemáticos basados en agentes
En el Instituto Niels Bohr, trabajamos con muchos métodos, uno de ellos son los llamados modelos basados en agentes, en el que se encuesta a personas individuales, cuando se encuentran con otras personas y posiblemente contraigan la enfermedad. Esto es contrario a los modelos epidémicos habituales, en el que solo se pueden examinar los efectos a nivel de población. Estos modelos permiten, a través de datos en las redes de personas individuales, para el examen de una clase más amplia de estrategias. Especialmente el comportamiento de personas individuales, como cuántos amigos o familiares tienen alrededor, sus rutinas diarias de movimiento y cosas por el estilo. Los modelos de epidemia habituales son mucho menos detallados y no nos permitirán captar el efecto de todos los cambios individuales en el comportamiento que todos estamos haciendo en estos días.
Hemos trabajado en estrecha colaboración con el efecto del seguimiento de contactos y la cuarentena. Los cálculos preliminares del grupo NBI indican que puede reducir la parte superior de la epidemia con la aplicación. 50%, si utiliza un seguimiento de contacto simple y un aislamiento de 5 días de los contactos recientes con una persona enferma confirmada. Mientras la persona infectada esté aislada en su casa, él / ella no contribuye significativamente a la propagación de COVID-19.
El efecto de esta estrategia de "contacto y cuarentena" se ilustra en la Figura 1.
La figura compara el número de infectados en una situación en la que la sociedad se abre completamente con una situación en la que se aplica el rastreo de contactos simultáneamente con una apertura completa. Es importante tener en cuenta que el número de infectados se puede mantener aún más bajo, si mantenemos algunas de las medidas de reducción de infecciones que ya conocemos, como la higiene de las manos y la limitación de grandes asambleas. El rastreo de contactos no es una medida que se aplique por sí sola.
Los modelos basados en agentes son herramientas universales
También se pueden examinar otras estrategias para limitar la propagación de la enfermedad con modelos basados en agentes. Los grupos vulnerables de personas pueden aislarse para protegerlos de la enfermedad y reducir significativamente la necesidad de cuidados intensivos. Las simulaciones preliminares indican que si todas las personas mayores de 60 años reducen sus contactos sociales en un 75%, reduce la presión máxima sobre las unidades de cuidados intensivos a solo un tercio. Si los abuelos además de esto eligen aislarse de sus nietos, lo más probable es que reduzca la necesidad de cuidados intensivos en otro 50%.
El objetivo por encima de todo de cualquier estrategia para limitar la propagación de la enfermedad es, por supuesto, para , reducir la presión sobre los sistemas sanitarios, cuando la epidemia alcanza su punto máximo. Un hecho revelador de la importancia de estos cálculos de la epidemia de COVID-19 es que si no se hacía nada, la necesidad de camas de cuidados intensivos sería app. 10.000, - y nuestra capacidad es solo una aplicación. 500.
Los parámetros inciertos de la enfermedad.
Si desea comprender las muchas predicciones inciertas de los medios de comunicación en estos días, Es una gran ventaja conocer los parámetros más importantes de la epidemia de COVID-19. A continuación se explican los tres parámetros más importantes.
La tasa de crecimiento de la enfermedad.
La tasa de crecimiento está directamente relacionada con la probabilidad de infección cuando dos personas se encuentran. La tasa de crecimiento simplemente dice cuánto por ciento crece la epidemia por día. Este parámetro se estima a partir del número de ingresos hospitalarios en Dinamarca. A nivel mundial, se estima mejor a partir del crecimiento del número de muertes por día. A nivel internacional, el nivel en cada país era del 20% al 40% al comienzo de la epidemia, - más alto en Italia y España. Un porcentaje de este tamaño es característico del crecimiento exponencial de una epidemia fuera de control. El distanciamiento físico y el bloqueo se trata de limitar la cantidad de contactos, por lo que esta tasa debería disminuir.
La presión de la infección:la famosa R
R describe el número promedio de personas infectadas por cada individuo infectado. R es proporcional a la probabilidad de infección cuando dos personas se encuentran. R se calcula a partir de la tasa de crecimiento y el tiempo que tarda una persona en infectarse hasta que vuelve a infectarse. Este intervalo de tiempo aún es incierto, pero se estima entre 3 y 7 días. Cuanto más corto sea el intervalo, el menor será R. Un número R pequeño es bueno, ya que da como resultado un máximo más bajo para la epidemia, y resulta más fácil para una población alcanzar la inmunidad colectiva. Con R =2, en principio, "sólo" necesitamos reducir a la mitad nuestros contactos sociales para llegar a R =1, donde la epidemia comienza a extinguirse. Con R =4 tendríamos que reducir nuestros contactos sociales cuatro veces más. Nuestro comportamiento general tendría que cambiar significativamente, si R es mayor. Esta es la razón por la que diferentes valores de R significan tanto para cómo se calibran los modelos, y sobre cómo deberíamos evaluar nuestro bloqueo en marzo. La mejor evaluación en este momento es que la presión de infección R cayó de la aplicación. 3 a la aplicación. 0.7 durante nuestro encierro.
La figura oscura
La figura oscura es una indicación de cuántas personas más infectadas hay, than what we know of. It depends on how and how much we test, and will vary from country to country. Serum tests, showing if people have produced antibodies against the disease are very useful, because they will tell us how many have had the disease. The dark figure is not important for predictions in the beginning of an epidemic, but it is extremely important later, in order to assess where we are in the duration of the epidemic. A large dark figure will say that the disease is less dangerous and that we are closer to herd-immunity. The Norwegian authorities estimate that the dark figure is so high that only 3 in 1000 will die when infected.
These parameters are used in epidemic models of all types, so not only in agent-based models. When we wish to examine strategies depending on networks and social behavior, the agent-based models are particularly useful. As more precise data become available, we hope to be able to produce even better models, yielding more precise predictions of the development of the epidemic.