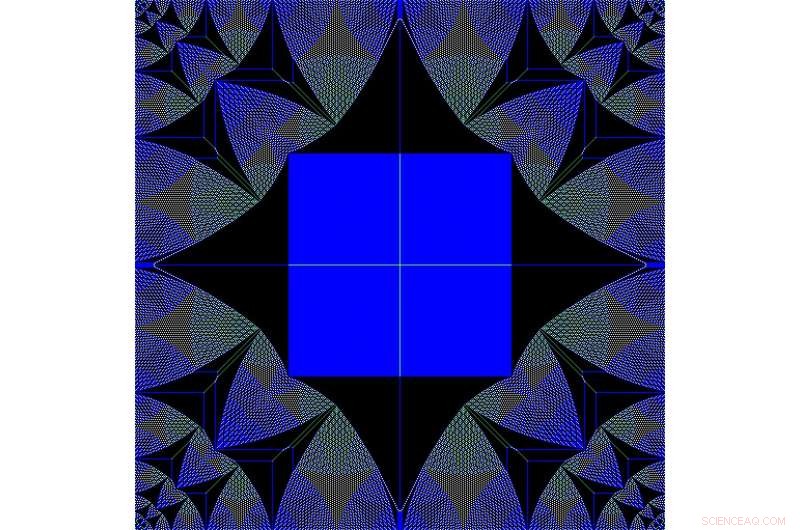
Patrones fractales en la pila de arena de Abelian. Crédito:Moritz Lang
El llamado modelo de pila de arena de Abelian ha sido estudiado por científicos durante más de 30 años para comprender mejor un fenómeno físico llamado criticidad autoorganizada. que aparece en muchas situaciones de la vida real, como la activación coordinada de células cerebrales, la propagación de los incendios forestales, la distribución de las magnitudes de los terremotos, e incluso en el comportamiento coordinado de las colonias de hormigas. Aunque el modelo de la pila de arena sirve como modelo arquetípico para estudiar la criticidad autoorganizada, Las preguntas sobre sus características siguen abiertas y siguen siendo un campo de investigación activo.
Moritz Lang y Mikhail Shkonikov del Instituto de Ciencia y Tecnología de Austria (IST Austria) han descubierto ahora una nueva propiedad de este modelo matemático:al agregar granos de arena de una manera específica a la pila de arena, Inducen dinámicas que recuerdan a la emergencia, movimiento, colisión y desaparición de dunas de arena en el desierto de Gobi o Namib. A diferencia de las dunas de arena del mundo real, sin embargo, las dunas en su trabajo están compuestas de patrones fractales auto-similares, algo similar al famoso set de Mandelbrot. Los resultados se publican en la edición actual de PNAS
Las reglas del "experimento de la pila de arena" son bastante simples:el modelo consiste esencialmente en una cuadrícula de campos cuadráticos, similar a un tablero de ajedrez, sobre el que se caen granos de arena al azar. Los campos que terminan con menos de cuatro granos de arena se mantienen estables, pero cuando se acumulan más granos en un campo, se vuelve inestable y se cae. En tal derribo, cuatro granos de arena se pasan a los cuatro campos vecinos:uno a la cima, uno al fondo, uno a la izquierda, y uno a la derecha. Esto puede hacer que los campos vecinos se vuelvan inestables y se derrumben, lo que a su vez puede hacer que los próximos vecinos se derrumben, y así sucesivamente, se produce una "avalancha". Similar a las avalanchas del mundo real en los Alpes, estas "avalanchas de pilas de arena" no tienen un tamaño característico, y es extremadamente difícil predecir si el próximo grano de arena causará una gran avalancha, o nada en absoluto.
De la simplicidad de estas reglas, el modelo de pila de arena se utiliza regularmente como un ejemplo sencillo en los cursos de programación elemental. Pero, sin embargo, muestra varios fenómenos matemáticos y físicos aún hoy inexplicables, a pesar de más de 30 años de investigación exhaustiva. Entre los fenómenos más fascinantes se encuentra la aparición de configuraciones fractales de pilas de arena. Estos montones de arena fractales se caracterizan por patrones auto-similares en los que las mismas formas aparecen repetidamente, pero en versiones cada vez más pequeñas. La aparición de estos patrones fractales aún no se ha explicado matemáticamente. Si bien los investigadores de IST Austria no resolvieron este acertijo matemático, Hicieron que el fenómeno fuera aún más misterioso al mostrar que estos patrones fractales aparentemente pueden transformarse continuamente entre sí:pudieron capturar videos en los que los patrones fractales muestran dinámicas que son, dependiendo de los antecedentes del observador, ya sea que recuerde el movimiento de las dunas de arena del mundo real, o de películas psicodélicas características de los años setenta.

Ilustración de la pila de arena de Abelian. Crédito:Moritz Lang
Profundizar en el misterio de una cuestión matemática puede no ser el resultado ideal. Sin embargo, los dos científicos, Moritz Lang y Mikhail Shkonikov, creen que sus "películas psicodélicas" podrían ser la clave para comprender mejor el modelo de la pila de arena, y quizás también de muchos otros físicos, problemas biológicos o incluso económicos.
"Se podría decir que hemos encontrado coordenadas universales para la pila de arena, "dice Mikhail Shkonikov". Esencialmente, podemos asignar a cada duna de arena del desierto un identificador muy específico ". Moritz Lang, quien es un biólogo teórico, agrega:"La clave para comprender cualquier fenómeno físico o biológico es comprender sus consecuencias. Cuantas más consecuencias sepamos, más difícil se vuelve desarrollar una hipótesis científica que esté de acuerdo con todas esas consecuencias. En ese sentido, conocer todas las dunas de arena posibles y cómo se mueven representa muchas limitaciones, y esperamos que al final, esto eliminará suficiente heno de la pila para que podamos encontrar la aguja ".
Los dos investigadores ven muchas aplicaciones en problemas del mundo real como la predicción de magnitudes de terremotos, el funcionamiento del cerebro humano, física, o incluso economía:"En todos estos campos, encontramos montones de heno que se parecen, muy similar. Tal vez resulte que todos los pajar son iguales, y que solo hay una aguja para encontrar ".