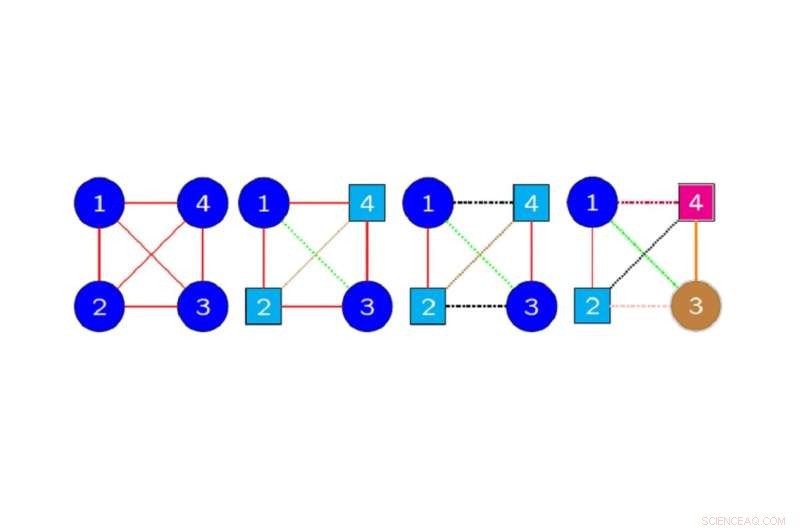
Ejemplos de gráficos de colores que designan simetrías de datos de cuatro dimensiones:Los vértices y los bordes del mismo color y forma en un gráfico se asignan entre sí mediante una permutación de simetría que preserva la estructura de los datos. Crédito:Hideyuki Ishi, Universidad Metropolitana de Osaka
Un equipo de investigación internacional dirigido por científicos de la Universidad Metropolitana de Osaka ha desarrollado un método para identificar simetrías en datos multidimensionales utilizando técnicas estadísticas bayesianas.
Este enfoque estadístico requiere cálculos complejos de integrales, que a menudo se consideran solo aproximaciones. En su nuevo estudio, el equipo de investigación obtuvo con éxito nuevas fórmulas integrales exactas. Sus hallazgos contribuyen a mejorar la precisión de los métodos para identificar simetrías de datos, posiblemente ampliando sus aplicaciones a áreas de interés más amplias, como el análisis genético.
Las simetrías en la naturaleza hacen que las cosas sean hermosas; las simetrías en los datos hacen que el manejo de datos sea eficiente. Sin embargo, la complejidad de identificar dichos patrones en los datos siempre ha sido un problema para los investigadores. Científicos de la Universidad Metropolitana de Osaka y sus colegas han dado un gran paso hacia la detección de simetrías en datos multidimensionales utilizando estadísticas bayesianas. Sus hallazgos fueron publicados en The Annals of Statistics .
La estadística bayesiana ha estado en el punto de mira en los últimos años debido a las mejoras en el rendimiento de las computadoras y sus posibles aplicaciones en inteligencia artificial. La estadística bayesiana es un enfoque estadístico que, incluso cuando los datos son insuficientes, deriva la probabilidad de que ocurra un evento estableciendo primero una probabilidad previa y luego, cada vez que se obtiene nueva información, calculando una probabilidad posterior (una actualización de la probabilidad previa) de que el ocurrirá el evento. El cálculo de probabilidades posteriores requiere cálculos complejos de integrales y, por lo tanto, a menudo se considera solo una aproximación.
El equipo internacional, que incluye al profesor Hideyuki Ishi de la Universidad Metropolitana de Osaka, el profesor Piotr Graczyk de la Universidad de Angers, el profesor Bartosz Kołodziejek de la Universidad Tecnológica de Varsovia y la difunta profesora Hélène Massam de la Universidad de York (Toronto), ha logrado obtener nuevas fórmulas integrales exactas. y en el desarrollo de un método para buscar simetrías en datos multidimensionales utilizando técnicas estadísticas bayesianas.
Cuando aumenta la cantidad de datos a manejar, se debe seleccionar el patrón óptimo entre una gran cantidad de patrones, lo que dificulta la resolución precisa del problema. Abordando este desafío, el equipo también ha desarrollado un algoritmo eficiente para obtener una solución aproximada incluso en tales casos.
En palabras del profesor Ishi, "las simetrías en los datos son omnipresentes en una amplia variedad de modelos. Una vez que se identifican las simetrías, la cantidad de parámetros necesarios para mostrar la estructura de los datos y la cantidad de muestras necesarias para determinar los parámetros pueden se reducirá significativamente En el futuro, se espera que los resultados de esta investigación contribuyan al análisis genético, descubriendo cromosomas que tienen la misma función en diferentes lugares". La selección del modelo bayesiano muestra un comportamiento extremadamente polarizado cuando los modelos son incorrectos