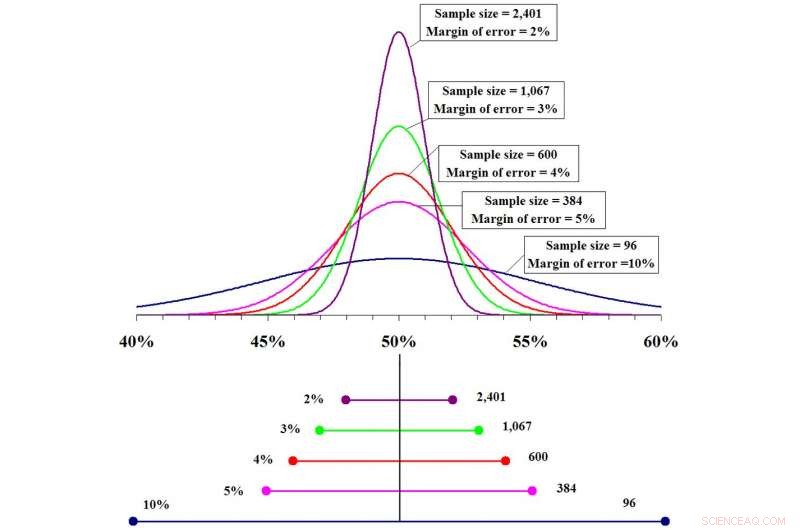
Cuanto mayor sea el tamaño de la muestra, cuanto más precisa sea la predicción y menor será el margen de error. Crédito:Fadethree a través de Wikimedia Commons
En el año pasado, las estadísticas han sido inusualmente importantes en las noticias. ¿Qué tan precisa es la prueba de COVID-19 que usted u otras personas están usando? ¿Cómo saben los investigadores la eficacia de las nuevas terapias para los pacientes con COVID-19? ¿Cómo pueden las cadenas de televisión predecir los resultados de las elecciones mucho antes de que se hayan contado todos los votos?
Cada una de estas preguntas implica cierta incertidumbre, pero aún es posible hacer predicciones precisas siempre que se comprenda esa incertidumbre. Una herramienta que utilizan los estadísticos para cuantificar la incertidumbre se llama margen de error.
Datos limitados
Soy un estadístico, y parte de mi trabajo es hacer inferencias y predicciones. Con tiempo y dinero ilimitados, Simplemente podría probar o encuestar a todo el grupo de personas que me interesan para evaluar la pregunta en mente y encontrar la respuesta exacta. Por ejemplo, para conocer la tasa de infección por COVID-19 en los EE. UU., Simplemente podría probar a toda la población de EE. UU. Sin embargo, en el mundo real, nunca se puede acceder al 100% de una población.
En lugar de, los estadísticos muestrean una pequeña parte de la población y construyen un modelo para hacer una predicción. Usando la teoría estadística, el resultado de la muestra se extrapola para representar a toda la población.
Idealmente, una buena muestra debe ser representativa de la población total, incluido el género, diversidad racial, diversidad socioeconómica, patrones de estilo de vida y otras medidas demográficas. Cuanto mayor sea la muestra, cuanto más similar sería a la población real, y con una muestra mayor, cuanto más confiados se vuelven los estadísticos en sus predicciones. Pero siempre habrá cierta incertidumbre.
Cuantificando la incertidumbre
Tomemos el desarrollo de fármacos, por ejemplo. Siempre es cierto predecir que un nuevo medicamento tendrá una efectividad de entre el 0% y el 100% para todos en la Tierra. Pero esa no es una predicción muy útil. El trabajo de un estadístico es reducir ese rango a algo más útil. Los estadísticos suelen llamar a este rango un intervalo de confianza, y es el rango de predicciones dentro del cual los estadísticos están muy seguros de que se encontrará el número verdadero.
Si se probó un medicamento en 10 personas y siete de ellas lo encontraron efectivo, la eficacia estimada del fármaco es del 70%. Pero dado que el objetivo es predecir la eficacia en toda la población, los estadísticos deben tener en cuenta la incertidumbre de probar solo a 10 personas.
Los intervalos de confianza se calculan mediante una fórmula matemática que abarca el tamaño de la muestra, el rango de respuestas y las leyes de la probabilidad. En este ejemplo, el intervalo de confianza estaría entre 42% y 98%, un rango de 56 puntos porcentuales. Después de probar solo a 10 personas, se podría decir con mucha confianza que el fármaco es eficaz para entre el 42% y el 98% de las personas en toda la población.
Si divide el intervalo de confianza a la mitad, obtienes el margen de error; en este caso, 28%. Cuanto mayor sea el margen de error, cuanto menos precisa sea la predicción. Cuanto menor sea el margen de error, cuanto más precisa sea la predicción. Un margen de error de casi el 30% sigue siendo un rango bastante amplio.
Sin embargo, Imagine que los investigadores probaron este nuevo fármaco en 1, 000 personas en lugar de 10 y fue eficaz en 700 de ellas. La eficacia estimada del fármaco seguirá siendo de alrededor del 70%, sin embargo, esta predicción es mucho más precisa. El intervalo de confianza para la muestra más grande estará entre el 67% y el 73% con un margen de error del 3%. Se podría decir que se espera que este medicamento tenga una eficacia del 70%, más o menos 3%, para toda la población.
A los estadísticos les encantaría poder predecir con un 100% de precisión el éxito o el fracaso de un nuevo medicamento o los resultados exactos de una elección. Sin embargo, esto no es posible. Siempre hay algo de incertidumbre y el margen de error es lo que cuantifica esa incertidumbre; debe tenerse en cuenta al analizar los resultados. En particular, el margen de error define el rango de predicciones dentro del cual los estadísticos están muy seguros de que se encontrará el número verdadero. Un margen de error aceptable es una cuestión de juicio basado en el grado de precisión requerido en las conclusiones a extraer.
Este artículo se ha vuelto a publicar de The Conversation con una licencia de Creative Commons. Lea el artículo original. 