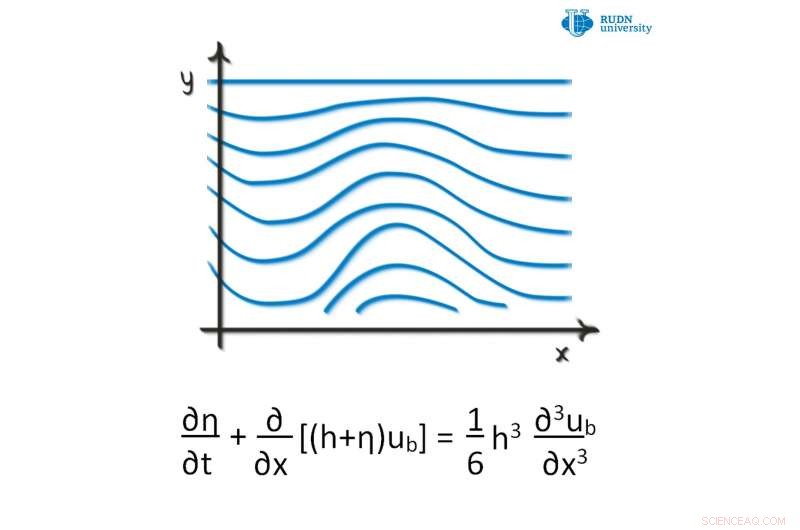
Un matemático de la Universidad de la RUDN propuso un nuevo criterio para resolver las ecuaciones de Boussinesq. Estas ecuaciones describen la propagación no lineal de ondas en ciertos medios, p.ej. plasma, una superficie de líquido de poca profundidad, etcétera. Examinaron la ecuación de Boussinesq en el espacio tridimensional y derivaron un criterio de unicidad y la existencia de soluciones importantes de un tipo especial para la ecuación diferencial parcial de Boussinesq. El criterio propuesto tiene aplicaciones en mecánica de medios continuos, que estudia el movimiento de líquidos y gases. El artículo fue publicado en Boletín de la Sociedad Brasileña de Matemáticas, Series nuevas .

Tanto las ecuaciones de Boussinesq como las ecuaciones de Navier-Stokes son sistemas de ecuaciones diferenciales parciales (la diferenciación se realiza con respecto a todas las variables independientes). Las ecuaciones diferenciales parciales juegan un papel importante en la física y la mecánica matemáticas. Resolver ecuaciones de este tipo a menudo está plagado de grandes dificultades. El problema de la existencia y unicidad de una solución a las ecuaciones de Boussinesq bajo condiciones iniciales dadas (el llamado problema de Cauchy) había sido previamente investigado por muchos científicos. incluidos los autores del artículo. Con ciertos valores de los parámetros, las ecuaciones de Boussinesq se convierten en ecuaciones de Navier-Stokes. La existencia y diferenciación continua, o, como dicen los matemáticos, suavidad, de soluciones a las ecuaciones de Navier-Stokes es uno de los siete problemas del Millennium Prize, planteado en 2000 por el Clay Mathematics Institute.

Para algunos espacios funcionales (a saber, para espacios Besov homogéneos, pf que los famosos espacios de Sobolev son un caso especial), el problema ha sido resuelto con éxito por los matemáticos Don y Zhang. La matemática de la Universidad RUDN Maria Alessandra Ragusa y su colega fueron más allá, demostrando un criterio similar para las ecuaciones de Boussinesq en espacios de Besov homogéneos. Los autores examinaron las ecuaciones de Boussinesq en un espacio tridimensional, lo que permite aplicar más plenamente los resultados en las ciencias naturales.

Habiendo introducido una serie de definiciones necesarias y lemas auxiliares probados, el autor de la Universidad RUDN demostró con éxito el teorema principal y demostró que la solución al problema de Cauchy no solo existe, es único, y no tiene puntos singulares, pero también se extiende suavemente a un intervalo mayor de una variable independiente. El artículo utiliza el aparato de análisis funcional, una disciplina matemática con un alto nivel de abstracción. Sin embargo, tales resultados pueden encontrar una amplia y fructífera aplicación en mecánica y física.