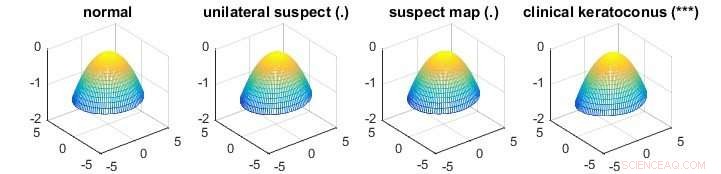
La figura demuestra una aplicación del nuevo método para identificar la diferencia de las superficies corneales medias con grados variables de la enfermedad del queratocono que causan deformaciones de las córneas. Los símbolos entre paréntesis después de los títulos de los grupos indican la significación estadística de la diferencia entre el grupo asociado y el grupo normal, donde "***" significa una diferencia muy significativa y "." sugiere una diferencia no significativa. El conjunto de datos de la córnea es un ejemplo de datos de alta dimensión. El grupo normal tiene 43 superficies corneales mientras que el sospechoso unilateral, mapa sospechoso, y los grupos de queratocono clínico tienen 14, 21 y 72 superficies corneales respectivamente. Cada superficie corneal tiene 6, 912 mediciones. Las pruebas tradicionales MANOVA no son adecuadas para este problema. Crédito:Universidad Nacional de Singapur
MANOVA (análisis multivariado de varianza) es un método estadístico comúnmente utilizado en el análisis de datos para determinar si existe alguna diferencia en las medias de los diferentes grupos de datos. Sin embargo, el enfoque clásico no es adecuado para analizar datos de alta dimensión. Los datos de alta dimensión a menudo invalidan los métodos MANOVA tradicionales, ya que en un MANOVA tradicional, se supone que la dimensión es fija y tiene que ser mucho menor que el número de observaciones. En un entorno MANOVA de altas dimensiones, Esto ya no es verdad. El profesor ZHANG Jin-Ting del Departamento de Estadística y Probabilidad Aplicada, NUS y su Ph.D. los estudiantes han desarrollado un nuevo método MANOVA de alta dimensión que se puede utilizar para comparar las medias de varios grupos de datos que involucran datos de alta dimensión de manera eficiente.
El nuevo método relaja muchas condiciones matemáticas y restricciones impuestas en la literatura. Uno de ellos es el supuesto de homocedasticidad. Esta suposición es una condición matemática que requiere que los datos de diferentes grupos tengan los mismos patrones de variación. Su nuevo método también resuelve los problemas computacionales involucrados en la implementación práctica de MANOVA para datos de alta dimensión. Para ello, utiliza cálculos matriciales de alto nivel computacionalmente eficientes.
Aunque es ampliamente aplicable y funciona bien para muchos conjuntos de datos de la vida real, el método propuesto puede ser menos eficaz en determinadas situaciones porque la información de variación y correlación de las variables no se utiliza en su totalidad. Al analizar los datos de la superficie corneal (consulte la figura siguiente), Se calcula la matriz de covarianza asociada que contiene la información de variación y correlación de los datos. Si el número de superficies corneales es mayor que el número de mediciones de una superficie corneal, la matriz de covarianza calculada es invertible, lo que significa que la estadística de prueba se puede obtener utilizando la prueba MANOVA tradicional. En un entorno de altas dimensiones, esto no es posible ya que el número de superficies corneales (150 =43 + 14 + 21 + 72 muestras) es mucho menor que el número de mediciones (6, 912 dimensiones). Sin embargo, la información de variación y correlación todavía se utiliza parcialmente para estimar los parámetros del estadístico de prueba. El profesor Zhang y su equipo de investigación están estudiando esto para desarrollar mejores métodos estadísticos que puedan manejar tales situaciones.