¿Se desintegrará cierto átomo de tritio en un tiempo determinado? Según nuestra ciencia actual, esta pregunta relativa a los fenómenos físicos debería responderse mediante un muestreo de una distribución de probabilidad, un proceso similar al de girar una ruleta o lanzar dados. Sin embargo, un artículo en Fundamentos de Física sugiere que lo mismo podría aplicarse a una pregunta relativa a fenómenos matemáticos, incluso uno tan prosaico como "¿qué es 2+2?"
El profesor de SFI David Wolpert, físico, y el ex becario de SFI Omidyar David Kinney, filósofo y científico cognitivo, proponen un marco probabilístico unificado para describir las matemáticas, el universo físico e incluso describir cómo los humanos razonan sobre ambos.
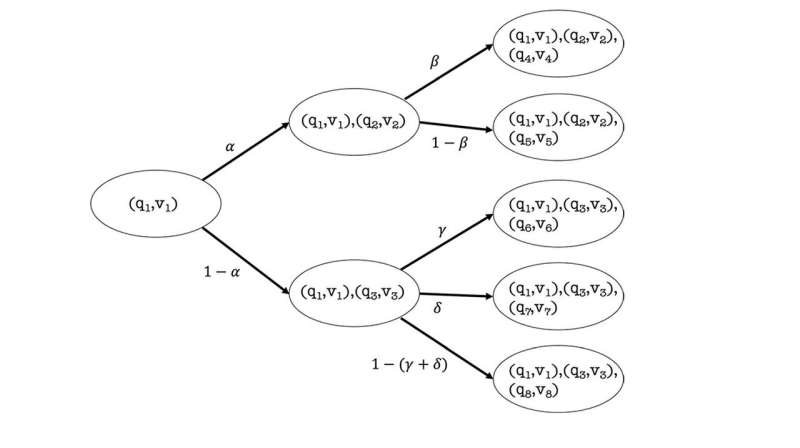
En su marco, las matemáticas y las ciencias se representan como un proceso de hacer y responder preguntas. La forma en que un matemático o científico determinado responda una pregunta dependerá de las probabilidades que asigne a las diferentes respuestas. En una extensión del formalismo básico, estas mismas probabilidades también determinan qué tan correctamente ese matemático o científico responde esas preguntas.
Para ilustrar, supongamos que usted responde una pregunta de matemáticas ahora y que, en un futuro lejano, algunos matemáticos responderán la misma pregunta. La exactitud de su respuesta depende de cómo sus probabilidades coincidan con las de ellos. (En física, su corrección implicaría experimentos físicos, no futuros físicos).
La aleatoriedad impregna cada parte del proceso de pregunta-respuesta, desde la selección de la pregunta hasta la respuesta dada. Esto da como resultado un beneficio importante del marco propuesto:una justificación formal novedosa para dos atajos de sentido común en ciencias y matemáticas:creer más firmemente en ideas respaldadas por múltiples líneas de evidencia y creer más firmemente en ideas que explican mejor algo. ya creo.
Más información: David H. Wolpert et al, Un modelo estocástico de matemáticas y ciencias, Fundamentos de la física (2024). DOI:10.1007/s10701-024-00755-9
Proporcionado por Instituto Santa Fe