¿Cuál es la mejor manera para que un grupo de individuos cooperen? Esta es una pregunta de larga data que tiene sus raíces en la teoría de juegos, una rama de la ciencia que utiliza modelos matemáticos sobre cómo los individuos deberían diseñar mejores estrategias para obtener un resultado óptimo.
Un ejemplo sencillo es el dilema del prisionero:dos personas son arrestadas por un presunto atraco a un banco. La policía los lleva al centro y los coloca en salas de interrogatorio individuales y aisladas.
La policía admite que no tiene pruebas suficientes para condenarlos a ambos y les da a cada uno la misma opción:si él confiesa y su compañero no, liberarán al confesor y condenarán al otro por el grave cargo de robo a un banco. Pero si uno no confiesa y el otro sí, el primero recibirá una larga pena de prisión y el otro quedará en libertad. Si ambos confiesan, ambos serán condenados a prisión por muchos años. Si ninguno de los dos confiesa, serán procesados por un cargo menor de posesión de armas.
¿Qué debería hacer cada uno para minimizar su tiempo en prisión? ¿Permanece un individuo en silencio, confiando en que su pareja hará lo mismo y acepta una pena de prisión más corta? ¿O confiesa, esperando que el otro guarde silencio? Pero ¿y si el otro también confiesa? Es una posición poco envidiable.
No existe una solución correcta al dilema del prisionero. Otros problemas similares son el juego de la gallina, donde cada conductor corre hacia el otro, arriesgándose a un choque frontal, o desviándose en el último minuto y arriesgándose a ser humillado:ser llamado "gallina" por falta de coraje. Existen muchos otros juegos sencillos.
Ahora imaginemos un grupo:pueden ser personas o pueden ser organismos celulares de algún tipo. ¿Qué tipo de cooperación da el resultado óptimo, cuando cada individuo está conectado con otros y paga un costo (dinero, energía, tiempo) para crear un resultado que beneficie a todos? Es un hecho que los individuos son egoístas y actúan en su propio interés, pero también sabemos que la cooperación puede resultar en un mejor resultado para todos. ¿Alguno correrá el riesgo o cuidará sólo de sí mismo?
Un resultado de larga data es que, en una red homogénea donde todos los individuos tienen el mismo número de vecinos, la cooperación se ve favorecida si la relación entre el beneficio proporcionado por un cooperador y el costo asociado pagado excede el número promedio de vecinos.

Pero las personas no son homogéneas, son heterogéneas y no suelen tener el mismo número de vínculos con sus vecinos que todos los demás ni cambian su estrategia al mismo ritmo.
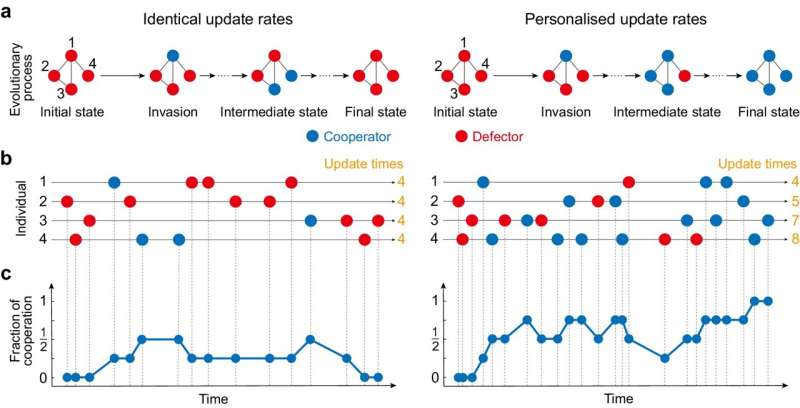
También se sabe que permitir que cada individuo actualice su estrategia exactamente al mismo tiempo, como por ejemplo imitar inmediatamente a su vecino, altera significativamente la evolución de la cooperación. Investigaciones anteriores han informado que las conexiones individuales heterogéneas generalizadas obstaculizan la cooperación cuando se supone que los individuos actualizan sus estrategias a ritmos idénticos.
Ahora, un grupo de investigadores ubicados en China, Canadá y Estados Unidos han encontrado un resultado sorprendente:cuando las tasas de actualización de estrategias de los individuos varían inversamente con su número de conexiones, las conexiones heterogéneas superan a las homogéneas en la promoción de la cooperación. El estudio se publica en la revista Nature Communications. .
"Cómo analizar el impacto cuantitativo de las estructuras de red heterogéneas predominantes en el surgimiento de estrategias óptimas de grupo es una cuestión abierta desde hace mucho tiempo que ha atraído mucha atención", dijo Aming Li, coautor y profesor asistente de Dinámica y Control en Universidad de Pekín.
El equipo de Li resolvió el problema mediante cálculos analíticos respaldados por simulaciones por computadora, para encontrar la regla fundamental para mantener la cooperación colectiva:"Los nodos con conexiones sustanciales dentro del sistema complejo deberían actualizar sus estrategias con poca frecuencia", dice. Es decir, las tasas de actualización de las estrategias individuales deben variar inversamente con la cantidad de conexiones que tienen en la red. De esta manera, una red con conexiones heterogéneas entre individuos supera a una red con conexiones homogéneas en la promoción de la cooperación.
El equipo también ha desarrollado un algoritmo que encuentra de manera más eficiente las tasas de actualización de estrategias óptimas que generan las estrategias óptimas del grupo, al que llaman OptUpRat. Este algoritmo ayuda a la utilidad colectiva en grupos y, dice Li, "también es esencial en el desarrollo de sistemas robóticos colaborativos". El hallazgo será útil para investigadores en campos multidisciplinarios como la cibernética, la inteligencia artificial, la ciencia de sistemas, la teoría de juegos y la ciencia de redes.
"Creemos que la utilización de técnicas relacionadas con la IA para optimizar las decisiones individuales e impulsar la inteligencia colectiva será el próximo punto de investigación".