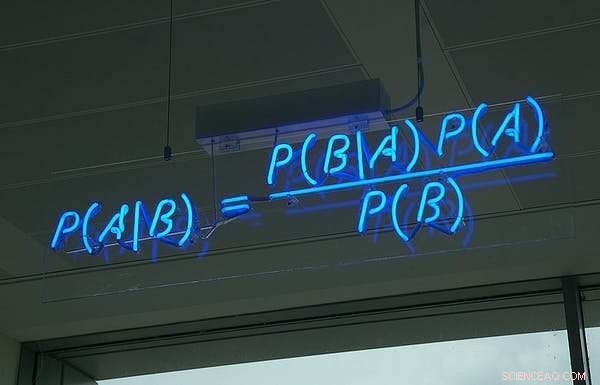
El teorema de Bayes, en neón, en la oficina de la empresa de software británica HP Autonony. Crédito:Wikimedia Commons, CC BY
Las inundaciones catastróficas de la costa este de Australia han sido descritas por el primer ministro de Nueva Gales del Sur como "un evento de cada 1.000 años, un término que ha creado una gran confusión".
Las extensas explicaciones de que estos términos no son lo mismo que "ocurriendo con 1000 años de diferencia" o "una vez cada 1000 años" solo han aumentado la confusión.
La explicación más simple es que el significado real de "uno en 1000 años" es "tener una probabilidad del 0,1 por ciento en cualquier año dado" (1 en 1000), lo que plantea la pregunta:¿por qué la gente simplemente no dice eso?
La razón principal es que estos términos se remontan a una época en la que la mayoría de la gente no pensaba en términos de probabilidades, e incluso aquellos que sí lo hacían estaban confundidos acerca de cómo funcionaban. En estos días interactuamos con probabilidades todo el tiempo.
El pronóstico meteorológico diario incluye un porcentaje de probabilidad de lluvia, y los pronósticos a más largo plazo brindan probabilidades de precipitaciones mayores o menores que el promedio de acuerdo con los ciclos de El Niño y La Niña.
Los mercados financieros apuestan por las probabilidades o los movimientos de las tasas de interés. La estadística y la probabilidad se enseñan a los niños en la escuela.
Pero esto es un desarrollo bastante reciente.
Hasta el siglo XVII se desconocían incluso los conceptos más elementales de la teoría de la probabilidad. La gente pensaba que el destino y la fortuna eran esencialmente incognoscibles. Incluso los jugadores no entendían las probabilidades.
El nacimiento de la probabilidad
De hecho, fue una solicitud de un amigo jugador alrededor de 1654 lo que motivó al filósofo y matemático francés Blaise Pascal a desarrollar los conceptos básicos de probabilidad con su colega matemático Pierre de Fermat.
(Pascal también usó la idea para desarrollar la "apuesta de Pascal" usada para demostrar la utilidad de creer en Dios. La idea es que si Dios existe, los creyentes serán recompensados con la bienaventuranza eterna. Si no, renunciarán a un número limitado de placeres terrenales mientras No importa cuán pequeña sea la probabilidad de que Dios exista, el beneficio de creer en Dios resulta ser infinito mientras que el costo es finito).
La comprensión se desarrolló lentamente. No fue hasta mediados del siglo XVIII que al clérigo inglés Thomas Bayes se le atribuyó el desarrollo más importante del campo.
La herramienta legada por Bayes
En su interpretación moderna, el teorema de Bayes nos brinda los medios para revisar nuestra visión de la probabilidad de un evento a la luz de la evidencia sobre lo que acaba de suceder.
Si algo acaba de suceder o no, se incluye explícitamente en el recálculo junto con evaluaciones actualizadas de la probabilidad de que eso importe.
Hasta Bayes, la mayoría de las probabilidades se calculaban como si no cambiaran, como la probabilidad de obtener "cara" al lanzar una moneda. Esas probabilidades podrían describirse de manera útil como "una en 1000 años" o "en promedio, cada segundo lanzamiento".
Pero la probabilidad de una inundación grave cambia con el tiempo a medida que cambia la relación entre los componentes que componen el sistema meteorológico. Si ha ocurrido una inundación nos da evidencia sobre ese cambio.
Esto hace que ya no sea útil referirse a una inundación severa como un evento "una en x años".
Ya pasó el momento en que cambiamos la terminología de una vez en tantos años, pero ¿a qué? La respuesta parece sencilla, aunque los detalles serán complicados.
Primero, necesitamos convertir las medidas antiguas en escalas de severidad, similares a las que se usan para ciclones y terremotos, pero específicas para cada cuenca.
Una vez hecho esto, la probabilidad de un evento de determinada gravedad puede estimarse sobre la base de la experiencia histórica y actualizarse a la luz de nueva evidencia.
¿Cómo se aplicaría esto en el caso de un evento como la inundación de Lismore?
La descripción inicial de "uno en 1000 años" significa que tal evento sería extremadamente improbable si la relación anterior se mantuviera.
Usando el teorema de Bayes, actualizaríamos la probabilidad inicial en 1,000 sobre la base de información actualizada sobre la posibilidad de que las relaciones subyacentes estén cambiando, produciendo nuevas probabilidades anuales cada año.
Así es como funciona el aprendizaje automático y cómo se actualizan las cuotas médicas y de seguros. Lamentablemente, las probabilidades revisadas casi seguramente excederán uno en 1,000.