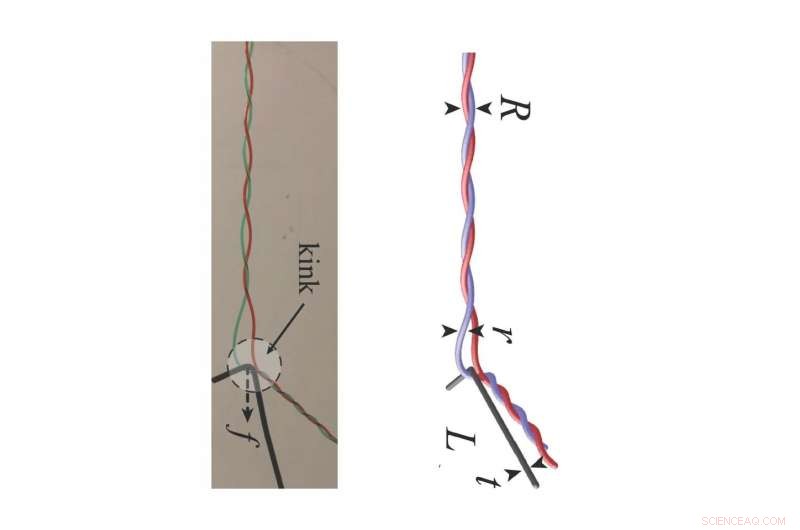
Los experimentos y simulaciones muestran que el diente se mueve a lo largo de la doble hélice desde el extremo sujeto hacia el extremo libre. Crédito:Harvard SEAS
Como sabe cualquiera que haya tenido que cepillarse el pelo largo, los nudos son una pesadilla. Pero con suficiente experiencia, la mayoría aprende los trucos para desenredar con la menor cantidad de dolor:comience desde abajo, avance hacia el cuero cabelludo con cepillos cortos y suaves, y aplique desenredante cuando sea necesario.
L. Mahadevan, Profesor Lola England de Valpine de Matemáticas Aplicadas, Biología Evolutiva y Organísmica y Física, aprendió la mecánica de peinar hace años mientras cepillaba el cabello de su pequeña hija.
"Recuerdo que el spray desenredante parecía funcionar a veces, pero aun así tenía que tener cuidado de peinar suavemente, empezando por las puntas libres", dijo Mahadevan. "Pero pronto me despidieron del trabajo porque no era muy paciente".
Si bien Mahadevan perdió su papel como peluquero, todavía era científico y la topología, la geometría y la mecánica del desenredado planteaban preguntas matemáticas interesantes que son relevantes para una variedad de aplicaciones, incluida la fabricación de textiles y procesos químicos como el procesamiento de polímeros.
En un nuevo artículo, publicado en la revista Soft Matter, Mahadevan y los coautores Thomas Plumb Reyes y Nicholas Charles exploran las matemáticas del peinado y explican por qué la técnica de cepillado utilizada por tantos es el método más efectivo para desenredar un manojo de fibras.
Para simplificar el problema, los investigadores simularon dos filamentos entrelazados helicoidalmente, en lugar de una cabellera entera.
"Usando este modelo mínimo, estudiamos el desenredado de la doble hélice a través de un solo diente rígido que se mueve a lo largo de él, dejando dos filamentos desenredados a su paso", dijo Plumb-Reyes, estudiante de posgrado en SEAS. "Medimos las fuerzas y deformaciones asociadas con el peinado y luego las simulamos numéricamente".
"Los trazos cortos que comienzan en el extremo libre y se mueven hacia el extremo sujetado eliminan los enredos creando un flujo de una cantidad matemática llamada 'densidad de enlace' que caracteriza la cantidad de hebras de cabello que se trenzan entre sí, de acuerdo con las simulaciones de la proceso", dijo Nicholas Charles, estudiante de posgrado en SEAS.
Los investigadores también identificaron la longitud mínima óptima para cada pasada:si era más pequeña, llevaría una eternidad peinar todos los enredos, y si era más larga, sería demasiado doloroso.
Los principios matemáticos del cepillado desarrollados por Plumb-Reyes, Charles y Mahadevan fueron utilizados recientemente por la profesora Daniela Rus y su equipo en el MIT para diseñar algoritmos para el cepillado del cabello por parte de un robot.
A continuación, el equipo tiene como objetivo estudiar la mecánica del cepillado del cabello más rizado y cómo responde a la humedad y la temperatura, lo que puede conducir a una comprensión matemática de un hecho que toda persona con cabello rizado conoce:nunca cepillar el cabello seco.