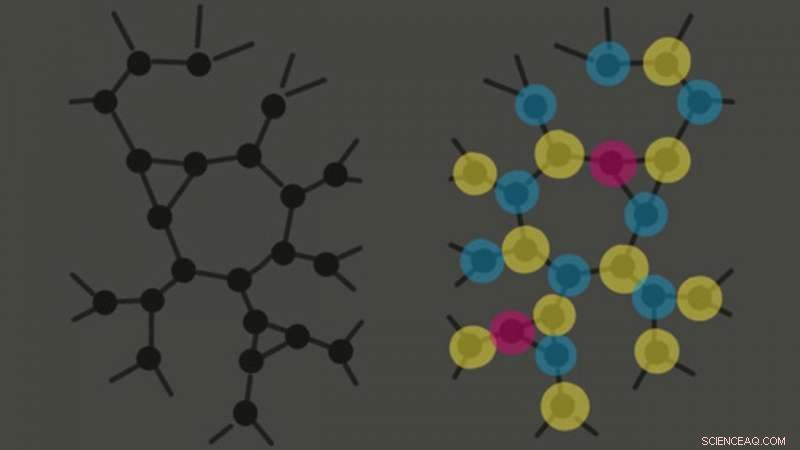
¿Pueden los algoritmos diferenciar estos dos gráficos? El gráfico uniforme de la izquierda es difícil de distinguir de la solución plantada de la derecha. Crédito:Jess Banks, presentación resumida en la Conferencia 2021 sobre Teoría del Aprendizaje
En informática, el problema de coloración de gráficos es un clásico. Inspirado por el problema de colorear mapas, pregunta:Dada una red de nodos conectados por enlaces, ¿Cuál es la cantidad mínima de colores que necesita para colorear cada nodo de modo que ningún enlace conecte dos del mismo color? Para pequeñas cantidades de colores y enlaces, buscar una solución es sencillo:simplemente pruebe todas las combinaciones posibles. Pero a medida que aumentan los enlaces, el problema se vuelve más limitado, hasta que, si hay demasiados enlaces y no hay suficientes colores, puede que no exista ninguna solución.
"Luego están estas fascinantes zonas intermedias donde probablemente haya una solución, pero es muy difícil de encontrar, y otro donde probablemente no lo haya, pero es difícil demostrar que no lo hay "dice el erudito Cris Moore, profesor residente en SFI. Eso significa que los algoritmos convencionales de resolución de problemas no pueden encontrarlos, él dice. Si uno comienza con una coloración aleatoria, por ejemplo, y comienza a cambiar los colores de los nodos, no encontrará una de estas soluciones ocultas.
En un nuevo artículo presentado en la Conferencia de Teoría del Aprendizaje de 2021, Moore y sus colaboradores describen una nueva forma de construir problemas con soluciones tan ocultas. El grupo incluye al matemático Jess Banks, un ex pasante de pregrado y posgrado de SFI que ahora está cursando un doctorado. en la Universidad de California-Berkeley.
Abordan el problema jugando a una especie de abogado matemático del diablo. En lugar de resolver problemas, hacen nuevos, los complicados, con soluciones ocultas en su interior. "Nos quitamos el sombrero blanco del solucionador, el buscador de soluciones, y nos ponemos el sombrero negro de la persona que diseña problemas complicados, casi como la criptografía, "dice Moore." La solución está oculta ".
Los investigadores idearon una forma sutil de ocultar soluciones, dice Moore. Y cuando transfieren estos problemas a algoritmos de resolución de problemas, los algoritmos aparecen vacíos. "Si podemos crear problemas que muchos algoritmos no pueden resolver, o incluso decir si hay una solución, "dice Moore, "Entonces tenemos pruebas sólidas de que hemos localizado la zona donde estos problemas son difíciles".
El artículo incluye un teorema que demuestra que múltiples familias de algoritmos no logran encontrar soluciones a estos problemas generados. Eso significa que los investigadores están más cerca que nunca de identificar el límite de transición de fase de esta zona "difícil" en la que es difícil encontrar soluciones, o demostrar que no las hay.
Moore dice que el esfuerzo continuo para identificar con precisión los problemas surgió de conjeturas en la física que preguntan cómo cambian los sistemas a medida que se vuelven más restringidos.
"Nuestra aventura, " él dice, "Ha sido convertir estas conjeturas y cálculos de la física en pruebas matemáticas". Y la única forma de seguir impulsando el campo hacia adelante, él dice, es recurrir a las fortalezas superpuestas de las herramientas de las matemáticas, física, y ciencias de la computación.