El 5 de enero Rosa Winter obtendrá su doctorado en geometría aritmética. Ella investigó soluciones de ecuaciones que definen las llamadas 'superficies del Pezzo "." Me gusta la geometría porque puedo imaginar y dibujar las formas y los objetos, ", dice Winter. Eso hace que las matemáticas abstractas se sientan más tangibles".

En matemáticas, a veces es útil estudiar ecuaciones abstractas utilizando objetos geométricos, como círculos, esferas octaedros, o incluso objetos de dimensiones superiores. El campo que conecta la geometría con las ecuaciones abstractas se llama geometría aritmética. Doctor. La candidata Rosa Winter aplicó este tipo específico de geometría en su tesis.

Dibujar superficies

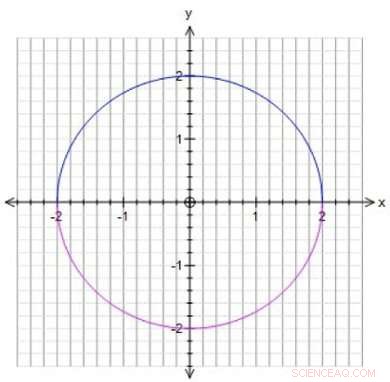
Las ecuaciones matemáticas pueden definir objetos geométricos, lo que significa que es posible estudiar soluciones a esas ecuaciones usando geometría. Por ejemplo, si desea saber qué números puede ingresar para que x ^ 2 + y ^ 2 sea igual a 4, puede dibujar todos los puntos (soluciones) para los cuales x ^ 2 + y ^ 2 =4. Esto da como resultado un círculo con radio 2, que muestra, por ejemplo, que el punto x =2, y =0 es una solución. También puede buscar soluciones específicas, puntos similares en el círculo donde xey son fracciones (1/3, 1/5, pero también, 0, 2, etc.). Esas soluciones fraccionarias se denominan puntos racionales. Winter estudió puntos racionales en superficies. "Las superficies son siempre bidimensionales, incluso si viven en ocho dimensiones, "dice Winter." Lo que significa que puedo dibujar superficies, haciendo que las matemáticas abstractas sean más intuitivas para mí ".

Pregunta del millón de dólares

Encontrar puntos racionales en objetos geométricos rara vez es fácil. Esto es mostrado, por ejemplo, por la llamada "conjetura de Birch y Swinnerton-Dyer". Esta conjetura matemática aún no probada es parte de los Problemas del Premio Milenio. El Clay Mathematics Institute otorga un millón de dólares para una correcta solución a cualquiera de estos problemas. La conjetura trata de puntos racionales en curvas elípticas. Como círculos Las curvas elípticas son objetos geométricos definidos por determinadas ecuaciones. Cuando los dibujas, parecen líneas curvas. Invierno:"Incluso en curvas elípticas, del que sabemos bastante, no es fácil determinar el conjunto de puntos racionales ".

Superficies Del Pezzo

Desafortunadamente, Winter no recaudó el millón de dólares durante su doctorado. investigar. Ella no trabajó en puntos racionales en curvas elípticas, pero en las llamadas superficies 'del Pezzo de grado 1. "Invierno:" Desde un punto de vista geométrico, estos no son los mas dificiles, superficies más complicadas, pero todavía tienen preguntas matemáticas sin respuesta ". Mostró para parte de esta familia de superficies que contiene un número infinito de puntos racionales que no se agrupan; se pueden encontrar dispersos alrededor de las superficies. Si los puntos racionales fueran visibles como puntos rojos y podías caminar sobre una superficie del-Pezzo, verías puntos racionales rojos dondequiera que mires.

Desde septiembre, Winter ha estado trabajando como postdoctorado en el Instituto Max Planck de Matemáticas en las Ciencias en Leipzig. Aquí ella aprende entre otras cosas, cómo aplicar la geometría y las matemáticas abstractas en otras ciencias, como la biología y la física.