Los matemáticos de la Universidad RUDN han estudiado las propiedades de los operadores compositivos en espacios con normas mixtas de Lebesgue. Su trabajo ayudará a describir la difusión de líquidos en materiales con grietas y en materiales porosos. Estos espacios también son útiles para obtener estimaciones de soluciones a la ecuación de Navier-Stokes. El artículo fue publicado en Notas matemáticas .

La ciencia moderna de las ecuaciones diferenciales parciales tiene su propia teoría:el lenguaje del análisis funcional. Los estudios de espacios funcionales en los que se buscan soluciones a ecuaciones comenzaron en el siglo XIX y han continuado hasta la actualidad. En primer lugar, Los matemáticos aprendieron a aplicar la teoría de Fourier a las soluciones de las ecuaciones diferenciales parciales lineales más simples, luego estudió los espacios de Banach y Hilbert, así como espacios de funciones generalizadas, que es esencialmente el lenguaje de la mecánica cuántica.

A mediados del siglo XX, Se descubrieron los espacios de Sobolev; estos ocupan ahora una de las posiciones centrales en la teoría de ecuaciones diferenciales parciales. Durante los próximos 50 años, ayudaron a los matemáticos a encontrar muchas soluciones a problemas aplicados que no se pueden encontrar en espacios funcionales ordinarios.

Más cerca del comienzo del siglo XXI, se hizo necesario encontrar nuevos métodos para estudiar ecuaciones diferenciales parciales no lineales, así se desarrollaron las matemáticas computacionales y la teoría de sistemas integrables. Sin embargo, Los métodos de estos campos resultaron estar demasiado enfocados, y la necesidad de desarrollar el idioma sigue ahí.

Los espacios de Lebesgue con normas mixtas son a veces objetos más universales y flexibles. Estos espacios se determinan de la siguiente manera:En el espacio de funciones en varias variables, definir la norma iterando la norma de Lebesgue. Inicialmente surgieron como una de las generalizaciones de los espacios de Sobolev y ya han despertado mucho interés por parte de teóricos de varios países de Europa, así como China, Canadá y Rusia.

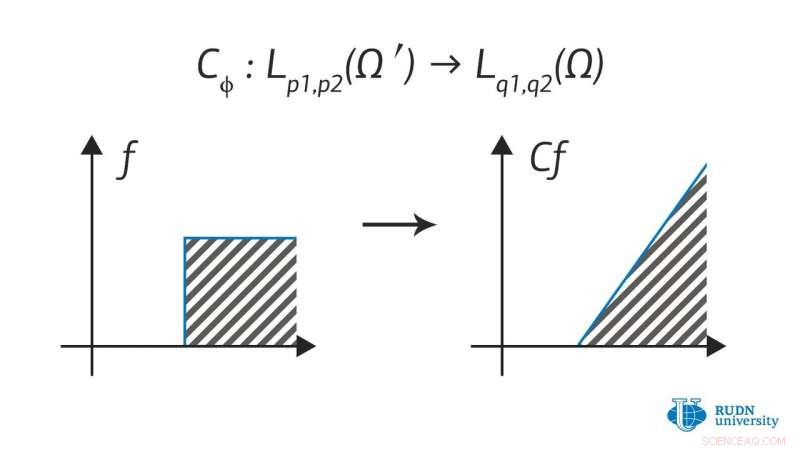
Nikita Evseev y Alexander Menovshchikov del Instituto Matemático de la Universidad RUDN trabajan en una teoría de operadores para tales espacios, lo que permite su uso en problemas aplicados formulados en el lenguaje de ecuaciones diferenciales parciales. Produjeron una gran cantidad de resultados nuevos que describen las propiedades de los operadores en dichos espacios:criterios para la delimitación de los operadores, propiedades de los operadores integrales, operadores de multiplicación, operadores de composición, y muchos otros. También obtuvieron algunos resultados auxiliares útiles para un mayor desarrollo de este campo.

"Nuestros métodos y resultados, creemos, se puede aplicar a problemas evolutivos y problemas diferenciales en regiones no cilíndricas. Por ejemplo, en biología (matemática), donde la superficie o el área en estudio cambia con el tiempo, o en hidrodinámica, para problemas con un límite variable, "dice Evseev.

La investigación en este campo es útil para estudiar las ecuaciones de Navier-Stokes, un sistema de ecuaciones que describen aerodinámica e hidrodinámica. Los espacios de Lebesgue con normas mixtas permiten evaluar soluciones, cuales, Sucesivamente, permite predecir la ausencia de turbulencias, por ejemplo.

Los resultados también ayudarán a estudiar los problemas aplicados de la física matemática que surgen en el estudio de materiales porosos y materiales con grietas. Por ejemplo, será posible predecir teóricamente el patrón de difusión y transferencia de calor en geles de sílice, vidrios porosos, varias esponjas, y espumas, así como en algunos materiales de construcción.