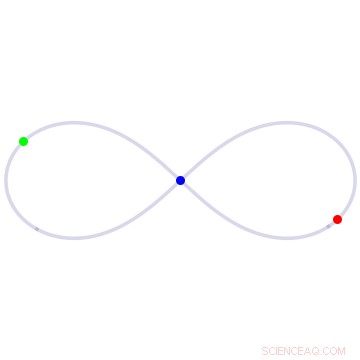
En la solución en ocho al problema de los tres cuerpos, tres cuerpos de igual masa persiguen cada uno alrededor de un bucle en forma de ocho. Crédito:Universidad de California - Santa Cruz
Desde sus orígenes hace más de 300 años en el trabajo de Newton sobre las órbitas planetarias, el problema de los tres cuerpos se ha convertido en un tema rico que sigue aportando nuevos conocimientos a los matemáticos.
Richard Montgomery, un distinguido profesor de matemáticas en UC Santa Cruz, lo llama uno de los dilemas clásicos de la historia matemática. En un artículo de la edición de agosto de Científico americano , relata la historia del problema de los tres cuerpos y el progreso que él y otros matemáticos han logrado en las últimas dos décadas.
"Ha desafiado a la gente durante siglos, y eso es en parte lo que lo hace interesante. Estás contribuyendo al trabajo de personas como Newton y Poincaré y Lagrange, "Dijo Montgomery.
El problema fundamental es predecir los movimientos de tres cuerpos (como estrellas o planetas) atraídos mutuamente por la gravedad, dadas sus posiciones y velocidades iniciales. Resulta que una solución general al problema es esencialmente imposible debido a la dinámica caótica, que Henri Poincaré descubrió en 1890.
"Hay soluciones para casos especiales, pero no existe una fórmula sencilla para ofrecerle una solución general, "Montgomery explicó.
Desde el punto de vista práctico de predecir órbitas planetarias y planificar misiones espaciales, las aproximaciones se pueden calcular con un alto grado de precisión utilizando computadoras y un proceso llamado integración numérica. Eso puede ser lo suficientemente bueno para la NASA, pero no para matemáticos, cuyas continuas exploraciones del problema han dado lugar a importantes avances en matemáticas.
Gatos que caen
El problema de los tres cuerpos une tres ramas diferentes de las matemáticas:topología, geometría, y dinámica. Montgomery dijo que eso fue lo que hizo que se interesara por él hace más de 20 años. Había estado trabajando en cuestiones relacionadas con las matemáticas y la física de cómo un gato aterriza de pie, que tiene aplicaciones en teoría de control y orientación satelital.
"Seguí simplificando el problema hasta que el gato consistió en solo masas de tres puntos, ", Dijo Montgomery. Luego, un colega lo refirió a otro matemático que había estado trabajando en ideas similares, y en poco tiempo había pasado de la caída de gatos a la mecánica celestial. Al enterarse de que las mejores personas que trabajan en mecánica celeste estaban en París, Montgomery pasó un año sabático trabajando con Alain Chenciner en la Universidad Paris Diderot sobre el problema de los tres cuerpos.
Uno de sus primeros resultados importantes, publicado en 2000, fue un redescubrimiento y prueba de una solución en forma de ocho, en el que tres cuerpos de igual masa se persiguen sin cesar alrededor de un bucle en forma de ocho. Aunque Chris Moore del Instituto Santa Fe había encontrado esta solución por primera vez en 1993, utilizando un método de aproximación numérica, su redescubrimiento por Montgomery y Chenciner tuvo un impacto mucho mayor en el campo.
"Pudimos dar una prueba de existencia rigurosa de la solución en forma de ocho, y la forma en que lo hicimos permitió a otros generalizar la solución y encontrar muchas otras cosas interesantes, "Montgomery explicó.
Un enunciado más general del problema de los tres cuerpos para cualquier número de cuerpos mayor que dos se denomina problema de N cuerpos. Montgomery dijo que cuando presentó por primera vez la solución de tres cuerpos en forma de ocho en una conferencia, un miembro de la audiencia señaló rápidamente cómo debería funcionar para cuatro cuerpos. Pronto, Los matemáticos estaban descubriendo una amplia gama de nuevas órbitas para el problema de cuerpos N de igual masa. Estas soluciones periódicas en las que todas las masas se persiguen alrededor de un fijo, curva cerrada sin colisiones fueron denominadas "coreografías" por el matemático español Carles Simó, que ha descubierto cientos de ellos.
"Creó una mini-industria, de modo que ahora conocemos un gran número de estas coreografías, "Dijo Montgomery.
Nueva dirección
Años después, Simó ayudó a enviar la investigación de Montgomery sobre el problema de los tres cuerpos en una nueva dirección sugiriendo que buscara mecanismos dinámicos subyacentes a las soluciones periódicas. Esto condujo a una colaboración productiva en los últimos años con Rick Moeckel de la Universidad de Minnesota.
Las nuevas ideas matemáticas que han surgido del trabajo de Montgomery sobre el problema de los tres cuerpos no tienen aplicaciones prácticas, al menos no todavía. A menudo ocurre que los conceptos matemáticos abstractos se desarrollan mucho antes de que alguien encuentre un uso práctico para ellos.
Muchas personas han quedado cautivadas por el atractivo estético de la solución en forma de ocho y otras coreografías. El concepto incluso se ha abierto camino en la ciencia ficción a través del autor chino Liu Cixin, cuya novela El problema de los tres cuerpos ganó el Premio Hugo en 2015.
Pero Montgomery dice que nunca habría abordado el problema si no hubiera tenido la titularidad.
"Es un problema tan difícil, y no sabes si vas a avanzar, ", dijo." Pero la persistencia a veces vale la pena. Por eso aprecio el sistema de tenencia, y también poder tomarse sabáticos para trabajar con colaboradores. Hay algo en conocer gente físicamente que es muy importante para trabajar juntos ".
En su Científico americano artículo, Montgomery proporciona no solo una descripción detallada del problema de los tres cuerpos, sino también una historia fascinante de las colaboraciones internacionales y las relaciones personales que le permitieron avanzar en este enigma matemático convincente.