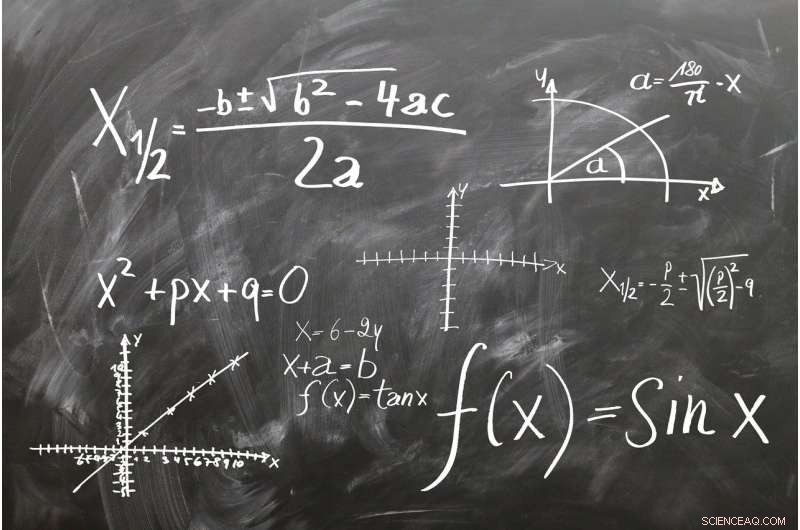
Crédito:CC0 Public Domain
Las matemáticas se consideran un instrumento que produce respuestas correctas a nuestras preguntas sobre el universo. Por ejemplo, las matemáticas pueden predecir correctamente que si tienes dos manzanas y comes una manzana al día, Te durarán precisamente dos días.
Sin embargo, a veces las matemáticas producen respuestas que parecen contrarias a la intuición de nuestras propias experiencias del universo, como la paradoja de Banach-Tarski, que establece que una bola sólida se puede cortar en varias piezas y estas piezas se pueden ensamblar en dos bolas sólidas, cada uno tiene el mismo tamaño que la bola original.
¿Sugieren estas contradicciones que hay una crisis en las matemáticas? que no puede explicar los misterios del universo? No. Simplemente nos obligan a reconsiderar cómo abordamos estos problemas.
Dar sentido al universo
Supongamos que estás en la orilla del mar con un niño y tienes un par de binoculares. Le entregas los prismáticos al niño y le sugieres que mire las gaviotas. Sin embargo, ella está mucho más interesada en ti que las gaviotas, así que en un minuto te apunta con los prismáticos, esperando ver una versión más grande de ti, y ella solo ve un borrón.
¿Les pasa algo a alguno de los dos? No. Hay algún problema con los binoculares. No. Su hijo simplemente usa los binoculares fuera del rango dentro del cual puede producir resultados significativos. Del mismo modo, Los enunciados contrarios a la intuición en matemáticas nos muestran los límites del rango útil de usar ciertas herramientas matemáticas.
Todos conocemos una paradoja matemática de nuestra infancia:no se puede dividir por cero. Esto se debe a que los números y las operaciones aritméticas son herramientas útiles, y es razonable combinar estas herramientas y utilizarlas juntas en la medida de lo posible.
Sin embargo, Las matemáticas no son una entidad armoniosa:sus herramientas encajan razonablemente bien, pero no del todo bien. Tenemos que cuidar la brecha entre ellos. La división es una herramienta útil, y cero es una herramienta útil, pero dividir por cero está más allá del rango útil de división.
Aparte de los hechos y las paradojas, Las matemáticas también pueden producir modelos inusuales que parecen intencionalmente separados del mundo que nos rodea. Consideremos un ejemplo muy simple. La siguiente imagen muestra una cuerda anudada. Sus extremos están pegados entre sí para evitar que se desate cuando se tira de una forma u otra.
No podemos desatar un nudo como este con solo tirar de él suavemente, tenemos que cortarlo. Sin embargo, un enfoque alternativo pregunta si un nudo se puede desatar considerándolo en algún espacio imaginario en lugar del espacio habitual. Por ejemplo, el nudo en la imagen de arriba es el llamado nudo rebanado, que se puede desanudar fácilmente si lo observamos en cuatro dimensiones espaciales, en lugar del espacio tridimensional al que estamos acostumbrados.
Respondiendo las preguntas de mañana
¿Por qué es importante para los matemáticos producir estos modelos inusuales? Una razón es crear un arsenal de modelos matemáticos que puedan usarse si la ciencia lo necesita en el futuro. En otras palabras, algunos de estos modelos pueden dejar de ser fantásticos y comenzar a tener perfecto sentido una vez que nuestro conocimiento del universo se ponga al día.
Más famoso, geometría no euclidiana, que fue desarrollado como un experimento mental por matemáticos a mediados del siglo XIX, argumentó que algunas líneas rectas pueden ser curvas. Se volvió indispensable para el descubrimiento de la teoría de la relatividad en el siglo XX, que argumentó que la luz, en lugar de viajar en línea recta, a veces viaja a lo largo de una curva, o incluso alrededor de un círculo.
También hay otra razón para estar al tanto de los modelos matemáticos inusuales. No todos estos modelos tienen la oportunidad de aplicarse directamente en las ciencias experimentales, pero todos pueden expandir nuestra imaginación y prepararnos adecuadamente para aceptar fenómenos científicos recién descubiertos. Esto es importante para apreciar la ciencia moderna.
Algunas personas no comprenden o no creen en el Big Bang. Lo más probable es que esto se deba a que su imaginación les falla cuando intentan imaginar un universo sin materia como lo conocemos y sin espacio como lo conocemos. Imaginar un espacio que no sea el mismo que percibimos puede resultar complicado. Por ejemplo, es difícil imaginar que, contrariamente a nuestra experiencia de primera mano, la Tierra no es plana.
Incluso si sabes que la Tierra es una esfera, Puede parecer extraño que haya lugares donde la gente camina "al revés". Si se da cuenta de que los matemáticos consideran constantemente y tratan con éxito modelos de espacio que desafían nuestra intuición, esto puede darle la confianza de que, si surge la necesidad, tanto la humanidad como usted pueden abordar cuestiones que desafían nuestra comprensión del espacio.
Este artículo se publicó originalmente en The Conversation. Lea el artículo original. 