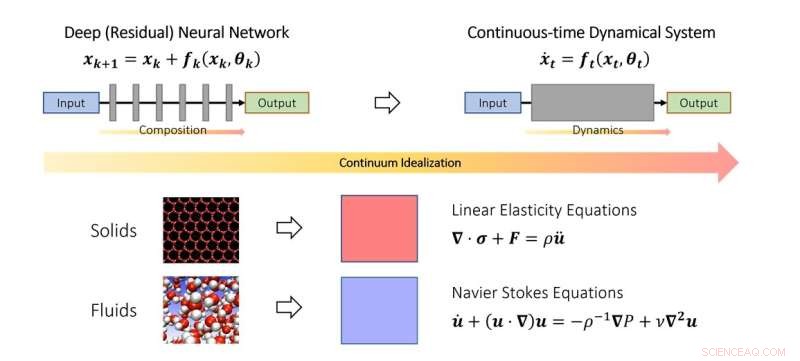
El punto de vista continuo del aprendizaje profundo. De manera similar a cómo los científicos estudian la mecánica de sólidos y fluidos en el límite continuo, también se pueden idealizar las redes neuronales profundas como una discretización de un sistema dinámico continuo. En el esquema, el parámetro de tiempo ficticio representa un análogo continuo de capas y la dinámica modela el apilamiento de capas. Crédito:Qianxiao Li
Los matemáticos de NUS han desarrollado un nuevo marco teórico basado en sistemas dinámicos para comprender cuándo y cómo una red neuronal profunda puede aprender relaciones arbitrarias.
A pesar de lograr un éxito generalizado en la práctica, comprender los principios teóricos del aprendizaje profundo sigue siendo una tarea desafiante. Una de las preguntas más fundamentales es:¿pueden las redes neuronales profundas aprender relaciones arbitrarias de entrada y salida (en matemáticas, se denominan funciones), y la forma en que lo logran difiere de las metodologías tradicionales?
Para entender esta pregunta, es necesario pensar qué es exactamente lo nuevo en las redes neuronales profundas en comparación con los paradigmas tradicionales de aproximación de funciones. Por ejemplo, la serie clásica de Fourier aproxima funciones complicadas como una suma ponderada de funciones más simples, como senos y cosenos. Las redes neuronales profundas funcionan de manera bastante diferente. En lugar de sumas ponderadas, construyen funciones complejas a partir del apilamiento repetido de funciones simples (capas). Esto también se conoce como composición de funciones en matemáticas. La pregunta clave es cómo se pueden construir funciones complicadas a partir de funciones simples apilándolas. Resulta que este es un problema bastante nuevo en la rama de las matemáticas conocida como teoría de la aproximación.
En este estudio publicado en el Journal of the European Mathematical Society , el profesor asistente Qianxiao LI del Departamento de Matemáticas de la Universidad Nacional de Singapur y sus colaboradores desarrollaron una nueva teoría de las capacidades de aproximación de la composición de funciones. Una observación interesante es que, si bien la composición de funciones es difícil de analizar en la práctica debido a su estructura discreta y no lineal, esta no es la primera vez que surgen tales problemas.
En el estudio del movimiento de sólidos y fluidos, a menudo se idealizan como un continuo de partículas, satisfaciendo algunas ecuaciones continuas (ecuaciones diferenciales ordinarias o parciales). Esto permite sortear la dificultad de modelar dichos sistemas a nivel atómico discreto. En cambio, se derivaron ecuaciones continuas que modelan su comportamiento a nivel macroscópico.
La idea clave del estudio es que este concepto se puede extender a redes neuronales profundas, idealizando la estructura en capas como un sistema dinámico continuo. Esto conecta el aprendizaje profundo con la rama de las matemáticas conocida como sistemas dinámicos. Tales conexiones permiten el desarrollo de nuevas herramientas para comprender las matemáticas del aprendizaje profundo, incluida una caracterización general de cuándo puede aproximarse a relaciones arbitrarias.
El profesor Li dijo:"El punto de vista de los sistemas dinámicos del aprendizaje profundo ofrece un marco matemático prometedor que destaca los aspectos distintivos de las redes neuronales profundas en comparación con los paradigmas tradicionales. Esto trae nuevos y emocionantes problemas matemáticos en la interfaz de los sistemas dinámicos, la teoría de la aproximación y el aprendizaje automático. "
"Un área prometedora de desarrollo futuro es ampliar este marco para estudiar otros aspectos de las redes neuronales profundas, como cómo entrenarlas de manera efectiva y cómo garantizar que funcionen mejor en conjuntos de datos invisibles", agregó el profesor Li. La red neuronal racional avanza en el aprendizaje de ecuaciones de diferenciación parcial