
Crédito:MarcoVector / Shutterstock
La enfermedad ha afligido a los humanos desde que existieron los humanos. Se cree que la malaria y la tuberculosis han devastado el Antiguo Egipto más de 5 años. Hace 000 años. Se estima que entre el 541 y el 542 d.C., la pandemia mundial conocida como "la plaga de Justiniano" mató entre el 15% y el 25% de los 200 millones de habitantes del mundo. Tras la conquista española de México, la población nativa se redujo de alrededor de 30 millones en 1519 a solo tres millones 50 años después. Hoy luchamos por controlar la propagación de COVID-19, que tiene el potencial de causar la pandemia más mortal en la historia de la humanidad.
Hay, sin embargo, un campo de la ciencia poco conocido pero de gran éxito que trabaja en segundo plano para desentrañar los misterios de las enfermedades infecciosas. Mientras exploro en Las matemáticas de la vida y la muerte, La epidemiología matemática está jugando un papel crucial en la lucha contra enfermedades infecciosas a gran escala como COVID-19.
Con modelos matemáticos básicos, los investigadores pueden comenzar a pronosticar la progresión de las enfermedades y comprender el efecto de las intervenciones en la propagación de la enfermedad. Con modelos más complejos, podemos comenzar a responder preguntas sobre cómo asignar eficientemente los recursos limitados o desentrañar las consecuencias de las intervenciones de salud pública, como cerrar pubs y prohibir reuniones.
Los conocimientos de los modelos matemáticos son vitales para garantizar que las autoridades puedan prevenir tantas muertes como sea posible. A medida que aumenta la pandemia de COVID-19, He aquí un vistazo al modelo que utilizan los expertos para intentar mantenerse un paso por delante del virus.
El modelo S-I-R
Uno de los modelos matemáticos más simples de propagación de enfermedades divide a la población en tres categorías básicas según el estado de la enfermedad. Las personas que aún no han padecido la enfermedad se denominan "susceptibles". Se supone que todos nacen susceptibles y capaces de infectarse. Quienes han contraído la enfermedad y son capaces de transmitirla a los susceptibles son los "infectivos". El tercer grupo se conoce eufemísticamente como la clase "eliminada". Estas son las personas que han tenido la enfermedad y se han recuperado y ahora son inmunes. o los que han muerto. Estos individuos "removidos" ya no contribuyen a la propagación de la enfermedad.
Esto se conoce como el modelo S-I-R. Desde el dengue en América Latina hasta la peste porcina en los Países Bajos y el norovirus en Bélgica, el modelo S-I-R puede proporcionar lecciones vitales sobre cómo prevenir la propagación de enfermedades.
Este modelo ilustra la importancia del aislamiento social para los infectados. Quedándose en casa hasta que se recupere por completo, efectivamente, se pasa de la clase infectada directamente a la clase eliminada sin contraer el virus. Esta simple acción puede reducir el tamaño de un brote al reducir las oportunidades de que la enfermedad pase a personas susceptibles.
El hecho de que un brote se propague o se extinga depende en gran medida de un único número que es exclusivo de ese brote:el número de reproducción básico.
Piense en una población que es completamente susceptible a una enfermedad en particular, al igual que la población mundial en diciembre de 2019, al inicio del brote de COVID-19. El número promedio de individuos previamente no expuestos infectados por un solo, portador de la enfermedad recién introducido se conoce como el número de reproducción básico, ya menudo denotado R₀ (pronunciado "R-nada" o "R-cero").
Si una enfermedad tiene un R₀ menor que uno, entonces la infección desaparecerá rápidamente a medida que cada persona contagiosa transmita la enfermedad, de media, a menos de otro individuo. El brote no puede mantener su propia propagación. Si R₀ es mayor que uno, el brote crecerá exponencialmente.
Explosión exponencial
Las primeras estimaciones del número de reproducción básico de COVID-19 lo sitúan entre 1,5 y 4, con un valor de al menos 2 en diciembre y enero. Con un número de reproducción básico de 2, la primera persona con la enfermedad se la contagia a otras dos, quien cada uno, de media, Transmitir la enfermedad a otras dos personas y luego a otras dos cada una, etcétera.
Este crecimiento exponencial es característico de la fase inicial de la infección. Si se permitía que la propagación continuara así, diez generaciones por la cadena de progresión, más de 1, 000 personas se infectarían. Diez pasos más adelante el peaje se elevaría a más de un millón.
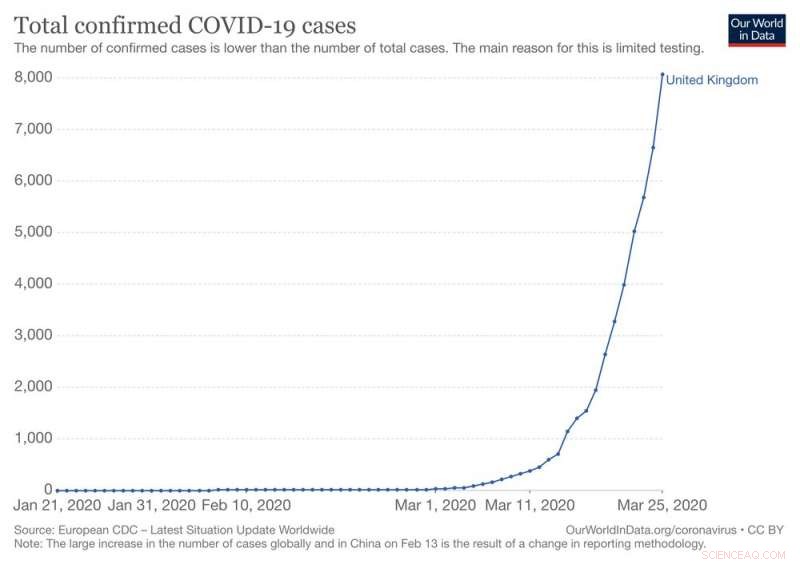
Los nuevos casos de COVID-19 en el Reino Unido han mostrado un aumento exponencial en los últimos días. Crédito:Max Roser, Hannah Ritchie y Esteban Ortiz-Ospina (2020) - 'Enfermedad por coronavirus (COVID-19) - Estadísticas e investigación', CC BY
En la práctica, el crecimiento exponencial predicho por el número de reproducción básico rara vez se mantiene más allá de unas pocas generaciones. Los brotes eventualmente alcanzan su punto máximo y luego disminuyen debido a la disminución de la frecuencia de contactos entre los infectados y los susceptibles.
Incluso cuando no queden agentes infecciosos y el brote haya terminado oficialmente, algunos susceptibles permanecerán. El modelo S-I-R puede proporcionar una estimación del tamaño final de la epidemia:la cantidad de personas infectadas al final de un brote si no se tomaron medidas correctivas. En el extremo inferior de las estimaciones de COVID-19, un número de reproducción de 1,5, significa que el 58% de la población se infectaría. En el extremo superior de las estimaciones, con un R₀ de 4, el modelo S-I-R predice que solo el 2% de las personas permanecerán sin infectar si no se toman medidas.
Un número crucial
El número de reproducción básico es útil para comprender casi cualquier brote porque reúne todas las sutilezas de la transmisión de enfermedades en una sola cifra. De la forma en que se desarrolla la infección en el cuerpo, al modo de transmisión, e incluso a la estructura de las sociedades en las que se propaga, captura todas las características clave del brote y nos permite reaccionar en consecuencia.
Normalmente, R₀ se puede dividir en tres componentes:el tamaño de la población, la velocidad a la que los susceptibles se infectan (a menudo conocida como la fuerza de la infección), y la tasa de recuperación o muerte de la enfermedad. El aumento de los dos primeros de estos factores aumenta R₀, mientras que aumentar la tasa de recuperación la reduce. Cuanto mayor sea la población y más rápido se propague la enfermedad entre los individuos, cuanto mayor sea la probabilidad de que sea el brote. Los individuos más rápidos se recuperan, cuanto menos tiempo tengan para transmitir la enfermedad a otros y, como consecuencia, más fácil será controlar un brote.
Luego está el eficaz número de reproducción. Este es el número promedio de infecciones secundarias causadas por un individuo infeccioso en un punto dado en la progresión del brote. Si, por intervención, el número de reproducción efectivo se puede reducir a menos de uno, entonces la enfermedad se extinguirá.
Tasa de letalidad
Aunque es crucial para el control de enfermedades, R₀ no nos dice qué tan grave es una enfermedad para una persona infectada. La proporción de personas infectadas que finalmente mueren a causa de una enfermedad se conoce como tasa de letalidad.
Una enfermedad extremadamente infecciosa como el sarampión, con un R₀ de entre 12 y 18, tiene una tasa de letalidad relativamente baja en comparación con el 50-70% de los pacientes con ébola que eventualmente morirán a causa de la enfermedad. Como resultado, Por lo general, el sarampión se considera menos grave que el Ébola, aunque el Ébola tiene un R₀ mucho menor de alrededor de 1,5. Las primeras estimaciones indican que la tasa de letalidad de COVID-19 está entre el 0,25% y el 3,5%.
Es importante recordar que la tasa de letalidad no es fija, depende de las respuestas de la sociedad y las personas a la enfermedad. así como sobre la demografía de la población que infecta. Por ejemplo, las tasas de letalidad de COVID-19 parecen variar significativamente con la edad del paciente, siendo los ancianos los más afectados.
Quizás sorprendentemente, las enfermedades con altas tasas de letalidad tienden a ser menos infecciosas. Si una enfermedad mata a muchas de sus víctimas con demasiada rapidez, reduce las posibilidades de que se transmita. Las enfermedades que matan a la mayoría de las personas que infectan y también se propagan de manera eficiente son muy raras. y generalmente se limitan a películas de desastres.
Aunque una alta tasa de letalidad aumenta significativamente los temores durante un brote, Las enfermedades con alto R₀ pero con una letalidad menor (piense en COVID-19 en comparación con el Ébola) pueden terminar matando a más personas en virtud del mayor número de personas que infectan.
Controlar un brote
Una de las opciones más efectivas para reducir la propagación de enfermedades es la vacunación. Al llevar a las personas directamente de susceptibles a eliminadas, evitando el estado infeccioso, reduce efectivamente el tamaño de la población susceptible.
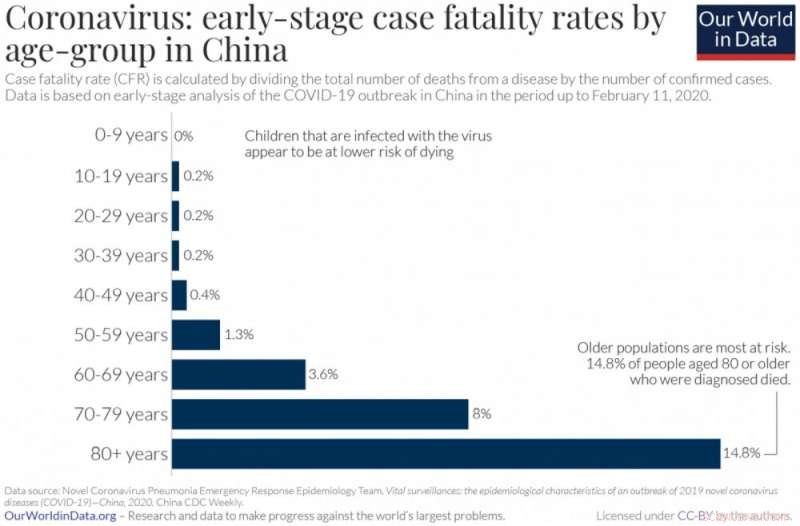
Las personas mayores tienen más probabilidades de morir por COVID-19 que la población en general. Crédito:Max Roser, Hannah Ritchie y Esteban Ortiz-Ospina (2020) - 'Enfermedad por coronavirus (COVID-19) - Estadísticas e investigación', CC BY
Pero la vacunación es típicamente una medida de precaución que se usa para reducir la probabilidad de que ocurran brotes en primer lugar. Una vez que los brotes como la pandemia actual de COVID-19 estén en pleno apogeo, A menudo, no es práctico desarrollar y probar una vacuna en un período de tiempo útil.
La cuarentena y el aislamiento pueden reducir de manera eficiente la tasa de transmisión y, como consecuencia, el número de reproducción efectivo. Aislar a los pacientes infecciosos reduce la tasa de propagación, mientras que poner en cuarentena a individuos sanos reduce la población susceptible efectiva.
Ambas acciones contribuyen a disminuir el número de reproducción efectiva, razón por la cual el distanciamiento social y el autoaislamiento son estrategias tan importantes para enfrentar el COVID-19.
La inmunidad de grupo
Una idea con la que el gobierno del Reino Unido parecía estar jugando en los primeros días de su respuesta fue la de la inmunidad colectiva:el concepto de que una gran población de individuos inmunes puede ralentizar o incluso detener la propagación de la enfermedad. Asombrosamente, Este efecto comunitario no requiere que todos sean inmunes a la enfermedad para que toda la población esté protegida. Al reducir el número de reproducción efectiva a menos de uno —asegurando que las personas infectadas entren en contacto con el menor número posible de personas susceptibles— se puede romper la cadena de transmisión y detener la enfermedad en seco. Crucialmente, La inmunidad colectiva significa que las personas inmunodeprimidas, los ancianos, las mujeres embarazadas y otros grupos demográficos de alto riesgo pueden beneficiarse de la protección que brinda la inmunidad de otras personas.
La fracción de la población que necesita ser inmune para proteger al resto varía dependiendo de cuán infecciosa sea la enfermedad. El número de reproducción básico, R₀, tiene la clave de cuán grande es esa proporción. Cuanto mayor sea el número de reproducción básico, cuanto mayor debe ser la proporción inmunitaria de la población. Por ejemplo, para una enfermedad con un número de reproducción básico de 4, el modelo S-I-R predice que las tres cuartas partes de la población deben ser inmunes. Si R₀ es tan bajo como 1,5, entonces potencialmente solo un tercio de la población necesita adquirir inmunidad para proteger a los dos tercios restantes.
Si hay una vacuna disponible, entonces se puede lograr la inmunidad colectiva vacunando a una proporción suficientemente alta de la población (dicho esto, solo hemos logrado erradicar por completo una enfermedad humana, la viruela, mediante la vacunación).
Cuando no hay una vacuna disponible, la única forma de que las personas adquieran inmunidad es infectarse con la enfermedad y recuperarse. Dada la tasa de letalidad de COVID-19, esto implicaría la muerte de muchos miles de personas. Como era de esperar, el gobierno del Reino Unido dio marcha atrás en su política propuesta.
La próxima generación de modelado
En realidad, el modelo simple S-I-R no es lo suficientemente complejo como para capturar las sutilezas de muchos brotes de enfermedades infecciosas. Pero para las enfermedades que no confieren inmunidad a sus víctimas, una simple adaptación del modelo S-I-R puede ayudar.
Como es típico de algunas enfermedades de transmisión sexual, la gonorrea no tiene población eliminada en absoluto. Una vez recuperado de la gonorrea, los pacientes pueden volver a infectarse. Dado que nadie muere por los síntomas de la gonorrea, nadie es nunca "eliminado" de la población. Estos modelos suelen tener la etiqueta S-I-S, imitando el patrón de progresión de un individuo de susceptible a infeccioso y de nuevo a susceptible de nuevo. Dado que la población de personas susceptibles nunca se agota, pero renovada a medida que la gente se recupera, el modelo S-I-S predice que las enfermedades pueden volverse autosostenibles o "endémicas".
Si una sola infección con SARS-CoV-2 (el virus que causa COVID-19) era suficiente para proporcionar inmunidad fue una de las principales preocupaciones de los científicos al comienzo del brote. ¿Podría el nuevo virus circular indefinidamente en la población? Aunque ha habido varios informes de personas que contraen el virus por segunda vez, También hay buena evidencia que sugiere que los pacientes con COVID-19 recuperados se vuelven inmunes.
Otro problema con el nuevo coronavirus es que suele haber un período asintomático al comienzo de la enfermedad. Durante este tiempo, las personas pueden albergar el virus e infectar a otros sin mostrar síntomas. Eso significa que debemos agregar otra clase de personas al modelo. Estas son personas que, una vez infectado, son capaces de transmitir la enfermedad sin mostrar síntomas, la denominada clase "portadora". Esto cambia el modelo S-I-R a un modelo S-C-I-R. La clase de portador es vital para representar enfermedades como el VIH / SIDA, que tienen largos períodos infecciosos sin síntomas evidentes.
Los modelos de vanguardia que se utilizan actualmente para informar las políticas gubernamentales son aún más complicados. Desafortunadamente, ni siquiera el modelo matemático más detallado y realista es capaz de predecir cuándo se pondrá fin a la pandemia actual.
Pero es cierto que cuando finalmente tomamos el control de la situación, Los matemáticos y sus modelos habrán jugado un papel importante en la forma en que se desarrolló el drama.
Este artículo se ha vuelto a publicar de The Conversation con una licencia de Creative Commons. Lea el artículo original. 