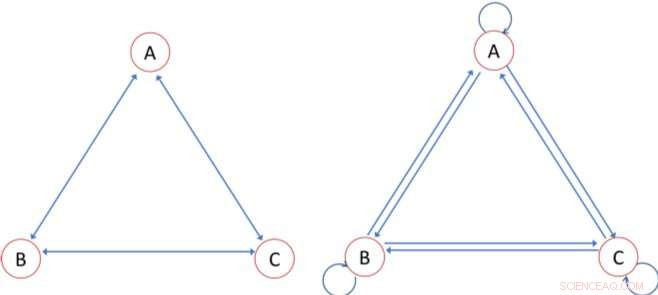
Diferencias experimentadas (panel izquierdo) y los bordes utilizados en la medida convencional (panel derecho). Si los nodos A, B, y C en la Figura 1 tienen riqueza 10, 4, y 3, por ejemplo, el coeficiente de Gini usando la representación de la red en el panel de la izquierda es 0.412. Usando la representación de red a la derecha, sin embargo, el Gini se estima en 0,274 Créditos:Samuel Bowles y Wendy Carlin
Una nueva forma de medir la desigualdad de la riqueza explica mejor la forma en que la experimentamos. En un artículo publicado en Cartas de economía , los economistas Samuel Bowles del Instituto Santa Fe y Wendy Carlin del University College London y el Instituto Santa Fe proponen un giro novedoso en el ampliamente utilizado coeficiente de Gini, una medida estadística de caballo de batalla para medir la brecha entre los que tienen y los que no tienen.
En una sociedad perfectamente igualitaria, donde todos los individuos son igualmente ricos, el coeficiente de Gini debería ser 0. Por el contrario, una sociedad donde un solo individuo posee toda la riqueza debe tener un coeficiente de Gini igual a 1. Usando el coeficiente de Gini, los países se pueden clasificar de menor a mayor desigualdad.
Pero la riqueza o los ingresos de las personas no son el panorama completo cuando se trata de desigualdad. Según Bowles y Carlin, el algoritmo estándar para calcular los coeficientes de Gini produce resultados extraños, por ejemplo, cuando un solo individuo posee toda la riqueza, el coeficiente de Gini es menor que 1, que es el valor que debería alcanzar con la máxima desigualdad. Corrigiendo ese error, ellos enseñan, requiere una solución basada en la red que tenga en cuenta las relaciones entre los individuos de la sociedad.
"Algunas de las dimensiones en las que se mide la desigualdad se conciben mejor como atributos individuales, de los cuales simplemente tienes más o menos, como la altura, ", explicó Bowles." Pero otras dimensiones, como la riqueza, se conciben mejor como diferencias entre las personas en sus relaciones con los demás ".
La red de la izquierda en la imagen representa el enfoque de Bowles y Carlin, donde las flechas que conectan los nodos representan interacciones sociales experimentadas. Por su medida, son las diferencias de riqueza en estos bordes, no la riqueza de cada nodo individual, que es la base de la desigualdad experimentada. En su papel Bowles y Carlin también que muestran el coeficiente de Gini correcto se calcula a partir de las tres diferencias asociadas con los tres bordes en la figura, y la riqueza media. Por ejemplo, digamos que el individuo A tiene una riqueza de 10, B tiene una riqueza de 4, y C tiene una riqueza de 3. Entonces, el coeficiente de Gini medido correctamente basado en las diferencias a lo largo de los tres bordes en la figura de la izquierda es 0.41.
El algoritmo estándar ilustrado en el diagrama de la derecha en la imagen cuenta la diferencia entre, decir, persona A y B dos veces (las dos flechas de una sola cabeza); pero surge un error en el algoritmo porque también cuenta la "diferencia" entre la riqueza de un individuo y su propia riqueza (las flechas curvas), que siempre es cero. Como resultado, el algoritmo estándar subestima el grado de desigualdad, produciendo un coeficiente de Gini de 0.27 para los mismos datos que arriba.
El error se nota solo cuando se trabaja con poblaciones pequeñas, como suelen hacer los arqueólogos y biólogos. En el caso de Carlin, un grupo de estudiantes de su clase de economía 101 le avisó del error cuando aplicaron un algoritmo estándar en línea para calcular los coeficientes de Gini a un conjunto de problemas. * El algoritmo que encontraron en línea de Wolfram arrojó diferentes respuestas para ejemplos con pequeñas cantidades de individuos de los encontrados aplicando la definición que representa el diagrama de red de la izquierda.
Bowles y Carlin también utilizan diferencias en la estructura de la red para analizar la experiencia de la desigualdad. Si los tres individuos de la red completa (a la izquierda) se reorganizaran en una línea, con la persona más rica en el centro, como podría representar un propietario con dos aparceros aislados, luego, sin cambios en la riqueza de los tres individuos, la desigualdad experimentada a lo largo de los bordes que conectan los tres aumentaría de 0,41 a 0,57.
Ilustran su método utilizando datos de redes sociales para estimar la desigualdad experimentada en una comunidad de agricultores en Nicaragua.
"Corregir el sesgo de los números pequeños no es la principal contribución de nuestro artículo, "dice Carlin." Es que hemos proporcionado una forma de entender la desigualdad consistente con nuestras intuiciones sobre cómo experimentamos las disparidades económicas, es decir, mediante la comparación por pares de la propia riqueza o los ingresos de uno con los de los demás ".