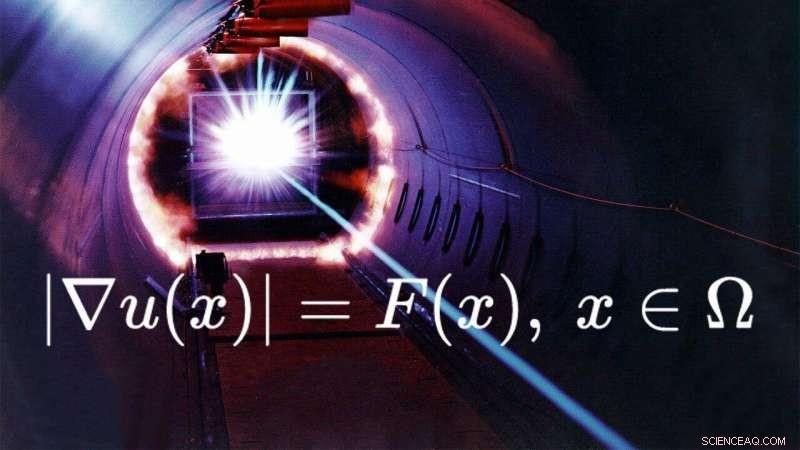
Crédito:Universidad RUDN
Los matemáticos de la Universidad RUDN y el Instituto de Seguridad Nuclear de la RAS (NSI RAS) han propuesto un método numérico para resolver ecuaciones que describen la propagación de la luz en un medio. Utilizaron la ecuación eikonal no lineal con condiciones de contorno como base. Tal problema no se puede resolver directamente, así que los matemáticos desarrollaron un método numérico, cálculos realizados, y produjo una imagen del "comportamiento" de tales soluciones. Los resultados podrían convertirse en la base para una teoría integral de soluciones aproximadas de tales ecuaciones diferenciales. El método se puede aplicar en la producción de lentes y cristales ópticos. El artículo fue publicado en Revista de matemáticas computacionales y aplicadas .
La ecuación eikonal es una ecuación diferencial parcial no lineal. Describe la propagación de la luz en un medio y es necesaria para resolver problemas en óptica. Permite conectar ópticas planas, enseñado en las escuelas, y óptica ondulatoria, que se describe mediante ecuaciones complejas.
Es tradicional utilizar un método basado en la resolución de un gran sistema de ecuaciones no lineales para encontrar una solución numérica (es decir, para obtener una solución aproximada suficientemente precisa) para la ecuación eikonal.
Los matemáticos de la RUDN University y NSI RAS utilizaron un enfoque diferente, lo que facilita encontrar una solución para la ecuación eikonal no lineal usando un método numérico:un cambio de variables con la adición de un parámetro. El cambio da como resultado nuevas ecuaciones, cuales, Por un lado, son más simples que los iniciales:el problema se vuelve lineal. Por otra parte, sus soluciones no son las soluciones del sistema original. Sin embargo, a medida que el parámetro disminuye, las soluciones para el nuevo sistema se acercan a las soluciones para el original.
Los matemáticos gradualmente (por un cierto valor fijo) disminuyeron el valor del parámetro agregado y para cada uno de esos valores resolvieron la ecuación numéricamente. Para cada valor de parámetro posterior, la solución resultante se comparó con las anteriores. A medida que el parámetro disminuyó, las soluciones cambiaron cada vez menos, es decir, el resultado de los cálculos se estabilizó. Resultó que una solución suficientemente estable requiere un valor de parámetro relativamente pequeño. La solución resultante se tomó como una aproximación de la ecuación original.
Los matemáticos han demostrado que tal método produce resultados bastante buenos en problemas de modelos representativos.
"La complejidad computacional, los llamados 'costos computacionales' del enfoque del que estamos hablando, no excede la de otros enfoques. Aunque, resolvemos un problema de valor límite lineal, y eso, por supuesto, es menos laborioso que resolver un problema no lineal, "explicó Petr Vabishevich, autor del estudio y miembro del Centro de Investigación de Métodos Computacionales en Matemática Aplicada de la Universidad RUDN.
Vabishevich y sus coautores modelaron la ecuación para medios anisotrópicos. Desde el punto de vista de la física, este es un entorno en el que las propiedades físicas de la propagación de la luz en diferentes direcciones no son las mismas. Los materiales con estas propiedades ahora se utilizan ampliamente en dispositivos ópticos.
Además de la óptica, la ecuación eikonal también se usa para resolver numéricamente ecuaciones que describen el movimiento de un fluido. Este modelo es necesario para crear imágenes realistas en gráficos por computadora, por ejemplo, en la película "Piratas del Caribe" el agua no solo fue dibujada sino calculada a nivel físico. La velocidad de cálculo, que potencialmente podría mejorarse con el método desarrollado por matemáticos de la Universidad RUDN y NSI RAS, juega un papel clave en estos casos.