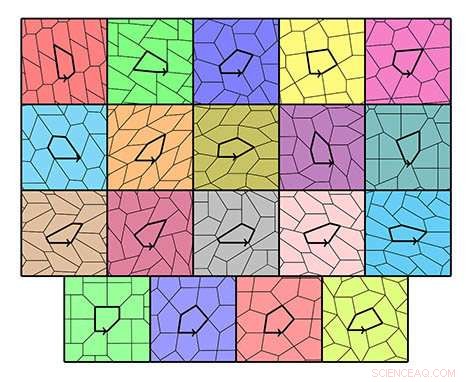
Los 15 tipos de baldosas pentagonales y sus 4 tipos específicos © Michael Rao, Laboratoire d'informatique du parallélisme. Crédito:CNRS / Inria / ENS Lyon / Université Claude Bernard Lyon
Colocar el plano en mosaico con un solo patrón es un problema matemático que ha interesado a los humanos desde la Antigüedad, especialmente por la calidad estética de las baldosas en mosaicos o alicatados. Uno de los problemas no resueltos en este campo que ha desconcertado a la comunidad científica desde 1918 se ha resuelto definitivamente gracias a Michaël Rao del Laboratoire d'informatique du parallélisme (CNRS / Inria / ENS de Lyon / Université Claude Bernard Lyon 1). Utilizando herramientas informáticas, pudo demostrar que solo hay 15 patrones de cinco lados que pueden enlosar el avión. La investigación ya está disponible en el Arxiv sitio web.
Hay una serie de soluciones para revestir un suelo con una sola forma, como triángulos, cuadrícula, rectángulos hexágonos etc. La búsqueda exhaustiva de todas las formas convexas que pueden enlosar el plano, una forma con ángulos menores a 180 ° que puede cubrir una pared entera sin superponerse, fue iniciada por Karl Reinhardt durante su tesis en 1918. Demostró que todos los triángulos y los cuadriláteros pueden enlosar el plano, pero que solo había 3 tipos de hexágonos que podían hacerlo, y que un polígono con siete lados o más no podría hacerlo. Solo quedaba abierta la cuestión de los pentágonos.
Se descubrieron 15 tipos de pentágonos entre 1918 y 2015 como parte de una investigación singular:iniciada por Reinhardt en 1918, pasó por una serie de giros y vueltas, como nuevos descubrimientos de matemáticos aficionados, hasta el anuncio mediatizado en 2015 de un nuevo 15º formulario 30 años después del 14º. Sin embargo, la comunidad científica aún no pudo determinar si había otras formas de pentágonos que pudieran enlosar el plano.
Michaël Rao, investigador del CNRS en el Laboratoire d'informatique du parallélisme (CNRS / Inria / ENS Lyon / Université Claude Bernard Lyon 1), ha demostrado definitivamente que sólo hay que tener en cuenta una serie finita de familias de pentágonos. Rao usó un programa de software para generar todas las posibilidades, y mostró que 371 familias de pentágonos podrían potencialmente enlosar el avión. Luego probó a cada una de estas familias usando otro programa, y demostró que solo 19 tipos de pentágonos cumplían las condiciones para los ángulos y longitudes de los lados requeridos para enlosar el plano. Entre estos 19 tipos, 15 correspondían a tipos ya conocidos, y los otros cuatro resultaron ser casos particulares de estos 15 tipos. Como consecuencia, solo 15 tipos de mosaicos pueden enlosar el avión.
Rao pudo resolver un problema centenario con su metodología, y abrir nuevas perspectivas. Todas estas baldosas convexas pueden revestir el plano periódicamente (es decir, los azulejos se repiten infinitamente). Sin embargo, aún no se sabe si existe un mosaico que permita el mosaico no periódico. Afortunadamente, la mayoría de estas técnicas también se pueden utilizar para polígonos no convexos, y, por tanto, podría servir de base para resolver otro problema en el campo del alicatado, más conocido como el "Problema de Einstein" (del alemán "ein stein").