Los patrones aparecen ampliamente en la naturaleza y las matemáticas, desde las espirales de Fibonacci de las conchas marinas hasta la periodicidad de los cristales. Pero ciertos problemas matemáticos a veces pueden engañar al solucionador humano para que vea un patrón, pero entonces, inesperadamente, el patrón desaparece repentinamente. Estos patrones ilusorios surgen en muchas áreas de las matemáticas, con un ejemplo proveniente de ciertas integrales de cálculo que han engañado la intuición incluso de los mejores matemáticos.

Ahora en un nuevo estudio, dos físicos se han acercado a estas integrales utilizando el concepto físico de paseos aleatorios. Mientras que resolver estas integrales generalmente requiere una gran cantidad de esfuerzo e ingenio, los físicos han demostrado que el nuevo enfoque puede encontrar soluciones de forma intuitiva y, a veces, incluso sin la necesidad de cálculos explícitos.

Los físicos Satya N. Majumdar y Emmanuel Trizac de la Universidad de Paris-Sud, CNRS, en Francia, han publicado un artículo sobre el uso de caminantes aleatorios para resolver integrales en un número reciente de Cartas de revisión física.

"Hemos demostrado que el conocimiento de la física nos permite obtener sin cálculos una gran cantidad de integrales curiosas, y además, para obtener identidades previamente desconocidas (ya sea integrales, o igualdades entre sumas discretas e integrales), "Trizac dijo Phys.org . "Nuestro trabajo revela que cuando se engaña la intuición matemática, la intuición física puede salvar el día ".

Patrones en integrales de Borwein

Las integrales en cuestión (ver figura) son "integrales de Borwein, "llamado así por David y Jonathan Borwein (padre e hijo), quien notó patrones inusuales en ellos en 2001. Las integrales de Borwein involucran el producto de funciones sinc (seno cardinal), que tienen aplicaciones muy extendidas, como en óptica, procesamiento de la señal, y otras áreas. Estas dos integrales particulares se pueden utilizar para calcular los volúmenes de hipercubos.

Resolver las integrales de Borwein implica sustituir números por la variable norte . Cada número da un valor de solución diferente, permitiendo a los matemáticos observar patrones en la secuencia de valores resultante. Por ejemplo, para la primera integral (yo _norte ), cuando sustituyes los números norte =1-7, obtienes la respuesta π cada vez. Pero cuando llegas a norte =8, la respuesta es ligeramente menor que π (aproximadamente π - 10 ^-10 ). La primera vez que los matemáticos calcularon este valor en una computadora, pensaron que debía haber un error en el software. Pero la respuesta fue confirmada, y los términos subsiguientes (para norte =9, 10, etc.) se vuelven cada vez más pequeños.

Algunos patrones persisten aún más. Para la segunda integral, J _norte , los primeros 56 términos de la secuencia (obtenidos sustituyendo los números del 1 al 56 por norte ) son todos π / 2. Pero el 57 ^th el término es aproximadamente π / 2—10 ^-110 , y los términos subsiguientes continúan disminuyendo. (Las cosas pueden volverse aún más extremas:para una variante de las integrales de Borwein, que no se discuten aquí, un patrón de valor constante es válido para unas asombrosas primeras 10 ¹⁷⁶ términos de la secuencia, después de lo cual el patrón finalmente se rompe.)

Los matemáticos pueden explicar por qué estos patrones se rompen repentinamente, al menos en términos matemáticos. Observe que las dos integrales de Borwein anteriores contienen la función sinc (a _norte k), donde un _norte =1 / (2n — 1). Si sustituye en los números 1, 2, 3, … por norte en esta expresión, obtienes la secuencia 1, 1/3, 1/5, 1/7, 1/9, ... Los Borwein notaron que el primer trimestre, 1, no solo es más grande que todos los demás términos que vienen después, pero es incluso mayor que la suma de los siguientes términos:del segundo al séptimo términos, para ser exacto, como 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 =0.955…, que es menor que 1. Pero al agregar el octavo término, 15/1, a esta suma, la respuesta es 1.02…, así que justo encima de 1. Resulta que no es una coincidencia que el séptimo término sea el último término para el que la integral se evalúa como π, y el octavo término es el punto en el que se rompe el patrón.

Borweins demostró un teorema (ver figura) que establece esta idea en términos más generales. El teorema es válido para la segunda integral, J _norte , así como. Contabilización de la función coseno en J _norte cambia la expresión anterior a 2 / (2n — 1), debido a la propiedad cos (a) sinc (a) =sinc (2a), de modo que el primer término sea 2 en lugar de 1. Como la suma del segundo hasta 56 ^th términos de la expresión es menor que 2, pero sumando el 57 ^th término empuja la suma por encima de 2, el teorema es válido.

Caminantes aleatorios

Aunque el teorema ayuda a explicar cuándo se rompen los patrones temporales de las integrales de Borwein, todavía no está completamente claro por qué el teorema es válido en primer lugar.

En el nuevo periódico, Majumdar y Trizac han ofrecido algo de intuición física en el teorema al conectarlo con algunos conceptos bien entendidos en teoría de probabilidad y mecánica estadística. Notaron que la integral en el teorema tiene vínculos estrechos con la distribución de probabilidad uniforme, que se usa ampliamente en toda la ciencia. Específicamente, la transformada de Fourier de la distribución de probabilidad uniforme resulta ser solo la función sinc, que produce la integral de Borwein para norte =1. Esta conexión une las integrales de Borwein con el mundo físico, de modo que mediante el uso de parámetros relevantes, Los eventos que siguen una distribución uniforme se pueden utilizar para modelar la secuencia de soluciones de las integrales de Borwein.

Para describir esta conexión en un contexto más físico, los investigadores observaron caminantes al azar. Un caminante aleatorio es un objeto abstracto que puede moverse una cierta distancia en cualquier dirección, donde la distancia exacta se elige al azar de un intervalo continuo de valores, y es igualmente probable que se elija cada uno de estos valores (es decir, sigue una distribución uniforme). Los caminantes aleatorios pueden modelar con precisión una variedad de fenómenos aleatorios, como los precios del mercado de valores, los caminos de los animales en busca de alimento, y los caminos de las moléculas en un gas, que ocurren en uno, dos, o tres dimensiones, respectivamente.

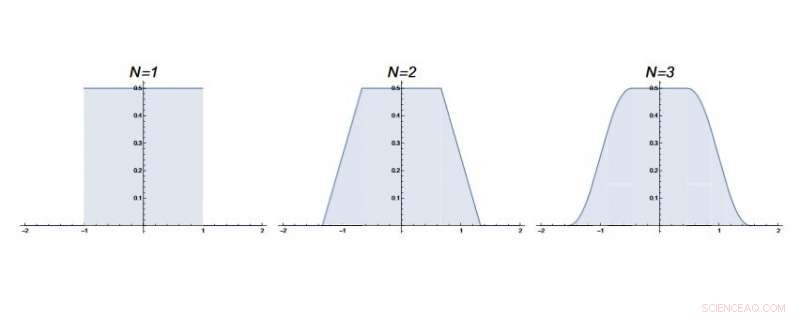
En el nuevo periódico, the physicists show that the movements of infinitely many random walkers can be used to model the emergence and disappearance of the patterns in the Borwein integrals. Empezar, the random walkers all start at the point zero on the one-dimensional number line. For the first step, each walker is allowed to move a random distance of up to 1 unit, either left or right. For the second step, each walker may move a random distance of up to 1/3, then a random distance of up to 1/5, then 1/7, 1/9, etc. That is, each successive allowable step distance corresponds to the next value of the expression 1/(2n—1).

The main question is, what is the fraction of random walkers at the starting point (the origin) after each time step? It turns out that the fraction (more precisely, the probability density) of walkers at the origin at each time step norte corresponds to the solution to the Borwein integral using the same norte valor.

As the physicists explain, for the first seven steps, the probability density that a walker ends up at the origin is always ½, which via the theorem above corresponds to an integral value of π. The key idea is that, up to this time, the density of walkers at the origin is the same as if the entire number line was uniformly populated with walkers. En realidad, as the maximum distance of each step is restricted, only part of the number line is accessible, es decir., the walkers' world is finite.

Sin embargo, for the first seven steps, the walkers at the origin perceive that their world is infinite, since they do not possess any information about the existence of boundaries that would indicate that the world is finite. This is because none of those walkers that reached the outer boundary of their world (+1 or -1 after the first step) would have been able to make it back to the starting point in less than seven steps, even if taking the maximum size steps allowed and all in the direction toward the starting point. As these walkers had zero probability of showing up at the starting point before the eighth step, they could not affect the fraction of random walkers at the starting point. So for the first seven steps, the density of walkers at the origin is fixed at ½ (it is "protected").

But once those walkers that have reached +1 or -1 return to the origin, the situation changes. After the eighth step, it's possible that some of these walkers return to the starting point. Now these walkers act as "messengers" in the sense that their return to the starting point reveals the existence of a boundary, telling the other walkers at the origin that their world is finite, and therefore influencing the density of walkers at the origin.

Since these messenger walkers made it back to the starting point, it becomes clear that some other boundary-reaching walkers did not make it back, but instead may have kept continuing to move further away. Como resultado, the probability distribution becomes more spread out, causing the fraction of walkers at the origin to gradually erode from ½ (or π for the integral). It is this erosion that explains why the values of the first Borwein integral decrease ever so slightly for n ≥ 8. A similar argument holds for the second Borwein integral (see video).

By connecting the Borwein integrals to the probabilities of random walkers, the new results offer a completely different approach to solving these integrals than through direct calculation. The physicists showed that the same approach can be applied to many other integrals in addition to the two described here, including extensions to higher dimensions. The researchers expect that the approach has the potential to provide calculation-free solutions to many other integrals that are otherwise very difficult to solve.

"Random walk problems and their infinite ramifications form one of the cornerstones of modern physics with a wide range of applications in physics, química, biología, Ingenieria, etc., " Trizac said. "Since our derivation of intriguing integrals involves basic concepts from random walk theory, we expect that new identities and integrals, with real-world applications, may be derived using our key idea in the near future."

© 2019 Science X Network