Investigadores de QUT que trabajan en problemas complicados en la agricultura, La ecología y la medicina han desarrollado un modelo matemático para permitir soluciones más rápidas.

Preguntas sobre la intervención, que tan fuerte y cuanto tiempo, son solo algunos de los juicios que enfrentan los médicos y científicos durante la toma de decisiones diaria.

Desde la producción de cultivos hasta la quimioterapia, nueva investigación publicada en Revista de la interfaz de la Royal Society , mejora la forma de determinar las "mejores" estrategias de intervención.

Profesor Matthew Simpson, Doctor. El investigador Jesse Sharp (en la foto a la izquierda) y el profesor Kevin Burrage del Centro de Ciencia de Datos de QUT y el Centro Australiano de Excelencia para Fronteras Matemáticas y Estadísticas (ACEMS) han desarrollado el nuevo método matemático para simular más rápidamente diferentes escenarios para alcanzar soluciones óptimas.

Señor agudo, que está estudiando su doctorado, dijo que el método implicaba una teoría de control óptimo que podría describirse como una "ciencia de compensaciones" entre objetivos en competencia.

"El uso de técnicas de optimización matemática nos ayuda a hacer más inteligentes, decisiones de asignación de recursos más eficientes, " él dijo.

"Si le administra a alguien demasiada quimioterapia, puede matar a la leucemia y al paciente. En ese caso, el 'costo' es obviamente demasiado alto, " él dijo.

Dijo que es importante encontrar el equilibrio adecuado entre los beneficios de la quimioterapia y los efectos secundarios perjudiciales.

"Haz una suposición, ejecutar ese escenario, utilizar técnicas matemáticas para mejorar su conjetura una y otra vez para acercarse cada vez más a la solución óptima, " él dijo.

"Lo que estamos haciendo es mejorar las técnicas numéricas, por lo que solo necesita resolver ese problema menos veces ".

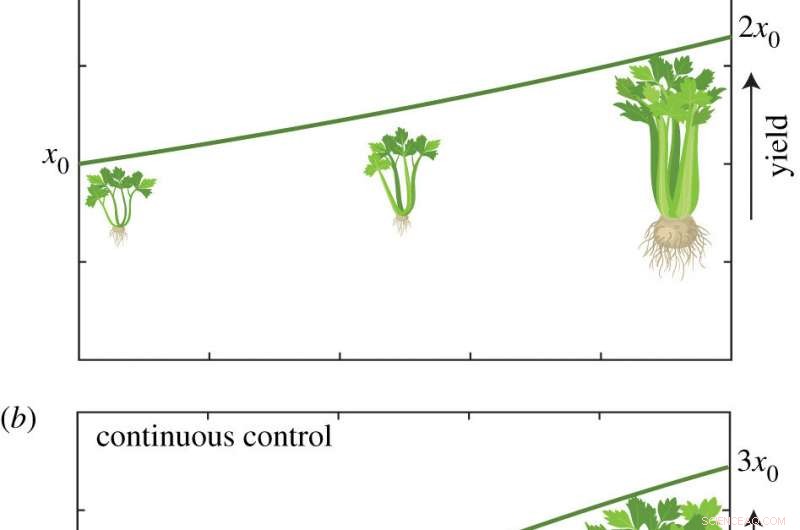
El método también se puede aplicar a las prácticas agrícolas (ver a la izquierda), para ver ejemplos en la determinación de opciones sobre cómo fertilizar cultivos.

La estrategia de control óptima que surge para una situación dada depende de cómo se caracteriza la optimalidad y qué significa el "mejor resultado" en el contexto de la situación específica.

Sharp dijo que la ilustración mostraba 'no control' como la estrategia más simple, mientras que el control 'bang bang' fue una intervención que cambió entre fertilizante máximo y sin fertilizante, mientras que en 'control continuo, "el fertilizante se puede aplicar en cualquier cantidad que puede cambiar con el tiempo.

"En esta investigación, mejoramos la eficiencia de las técnicas computacionales que se utilizan actualmente para resolver estos problemas de optimización, " él dijo.

"La eficiencia mejorada puede permitirnos abordar problemas más complejos que anteriormente pueden haber sido demasiado costosos desde el punto de vista computacional y demasiado lentos de resolver".

El profesor Matthew Simpson dijo que la investigación se puede aplicar a una variedad de problemas.

"Podemos encontrar una solución más rápido que antes, o podemos encontrar una solución donde los métodos computacionales no han podido encontrar una solución en el pasado, "Dijo el profesor Simpson.

"Siempre que tenga algún tipo de sistema para el que desee una salida, por lo que podría ser algo como un automóvil autónomo o algún sistema biológico, esta es una estrategia que puede indicarle los protocolos óptimos ".