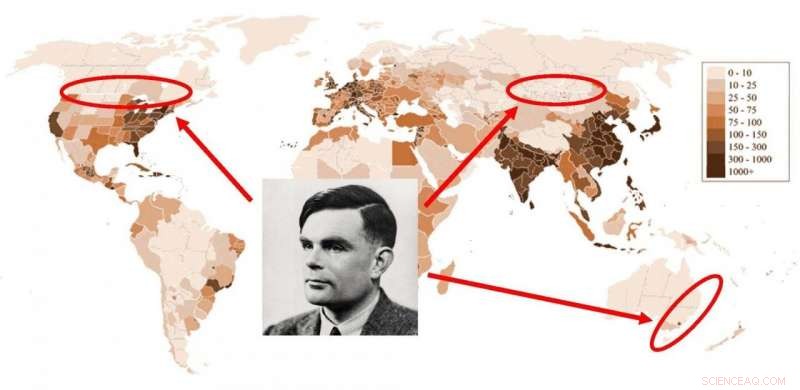
La teoría de la formación de patrones de Alan Turing puede explicar la distribución de la población humana en todo el mundo. Crédito:Universidad de Leicester
El rápido crecimiento de la población humana mundial se ha considerado durante mucho tiempo como un gran desafío al que se enfrenta la humanidad. Ahora, este desafío se está volviendo aún más serio que antes, en particular porque se estima que muchos recursos naturales se agotarán antes de finales de este siglo.
Se prevé que la creciente presión demográfica sobre la agricultura y los ecosistemas y el medio ambiente en general dará lugar a una escasez mundial de alimentos y agua. polución, falta de vivienda, pobreza y tensión social. La situación se ve agravada por el cambio climático global, ya que se prevé que grandes extensiones de tierra se inundarán y, por lo tanto, quedarán fuera del uso humano.
Se cree ampliamente que, a menos que se identifiquen e implementen escenarios alternativos de crecimiento poblacional sostenible y desarrollo social, es probable que la humanidad experimente un estancamiento o incluso un declive.
El crecimiento de la población en el tiempo se complementa con la dinámica de la población en el espacio. La distribución de la población en el espacio es enormemente heterogénea por una variedad de razones, por mencionar el clima, la historia y la economía son pocas. La heterogeneidad espacial puede resultar en importantes flujos migratorios que a su vez pueden tener una retroalimentación significativa sobre la demografía local y el crecimiento de la población.
En una escala más pequeña de países y estados individuales, Es necesario comprender los factores que afectan la distribución de la población en el espacio para garantizar el desarrollo adecuado de la infraestructura. Red de transporte y energía.
Es probable que las decisiones mal informadas provoquen hacinamiento y problemas sociales en las zonas urbanas y / o una menor calidad de vida en los barrios rurales. La identificación de escenarios de crecimiento poblacional sostenible y desarrollo social en diversas escalas espaciales y temporales requiere una buena comprensión de los procesos y mecanismos relevantes que afectan tanto al crecimiento poblacional como a la distribución de la población. Posiblemente, Es poco probable que tal comprensión se logre sin una teoría bien desarrollada y el marco matemático / de modelado correspondiente.
En efecto, Los modelos matemáticos de la dinámica de la población humana tienen una larga historia que se remonta al siglo XVII. Durante las últimas décadas, La necesidad de una teoría matemática adecuada y eficiente de la dinámica de la población humana se ha reflejado en un crecimiento constante en el número de estudios en los que se consideraron problemas de demografía junto con cuestiones relacionadas con la economía utilizando modelos matemáticos. Herramientas y técnicas.
En nuestro artículo reciente, utilizamos modelos matemáticos para abordar el fenómeno de la distribución espacial heterogénea de la población. Heterogeneidad de accidentes geográficos (montañas, bosques ríos etc.) y recursos naturales (por ejemplo, carbón, hierro y mineral de cobre) se aceptan comúnmente como factores que conducen a la heterogeneidad demográfica y económica.
Aquí hacemos una pregunta:¿es esta heterogeneidad natural la única causa subyacente, ¿O puede haber otro principio, quizás más general, responsable del surgimiento de una distribución heterogénea de la población? Para responder a esta pregunta, Primero revisamos los datos disponibles sobre la densidad de población en algunas áreas en diferentes partes del mundo para mostrar que, en todos los casos considerados, la distribución de la población exhibe un patrón espacial claro casi periódico a pesar de que las condiciones ambientales son relativamente uniformes. Inspirado por este hallazgo, luego consideramos un modelo novedoso de dinámica económico-demográfica acoplada en el espacio y el tiempo y tratamos de utilizarlo para simular la distribución espacial de la población. El modelo consta de dos ecuaciones diferenciales parciales acopladas de tipo reacción-difusión.
Siguiendo enfoques de modelado similares que se utilizaron con éxito en ecología y biología, mostramos que la aparición de patrones espaciales en nuestro modelo parece ser posible como resultado de la inestabilidad de Turing.
Aunque no es nuestro objetivo proporcionar una comparación directa entre los patrones demográficos del mundo real y las propiedades del modelo, Consideramos el acuerdo cualitativo entre las predicciones del modelo y los datos sobre la densidad de población humana como una indicación de que la distribución heterogénea de la población observada en diferentes países en diferentes continentes puede, al menos en algunos casos, han sido causadas por factores endógenos más que exógenos, es decir, puede haber aparecido debido a la inestabilidad intrínseca de Turing del correspondiente sistema dinámico económico-demográfico.
En muchos países, la distribución de la población en el espacio es claramente heterogénea, p.ej. las áreas urbanizadas con alta densidad poblacional se alternan con áreas rurales con baja densidad poblacional. Aparentemente, La variación espacial de los factores geográficos y climáticos puede desempeñar un papel importante en la configuración de la distribución de la población.
Nuestra principal hipótesis en nuestro trabajo es la existencia de un mecanismo dinámico que puede conducir a la formación de una distribución poblacional heterogénea independientemente de la heterogeneidad geográfica. En nuestra búsqueda de ejemplos del mundo real, nos centramos en los casos en los que se puede considerar el medio ambiente, hasta una cierta escala espacial, como relativamente uniforme. Las propiedades ambientales que consideramos aquí como sustitutos de la heterogeneidad ambiental son la elevación, la temperatura media anual y la precipitación media anual.