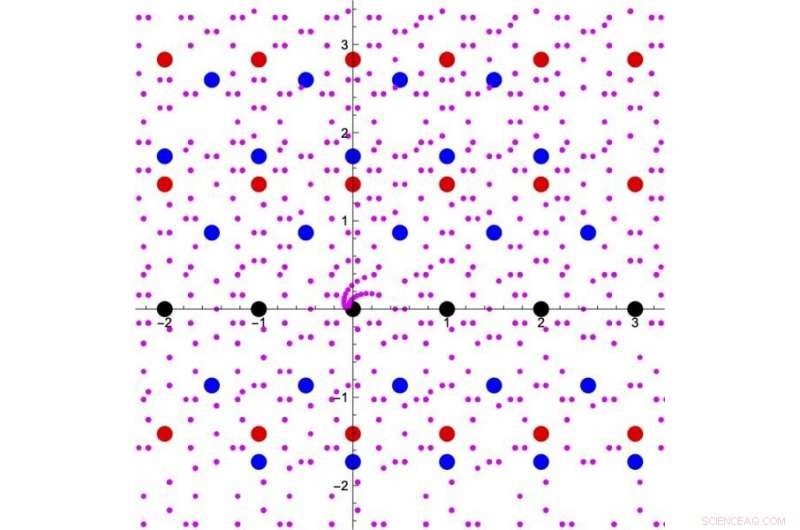
Figura 1. Ampliación del concepto de "números" integrales. Los puntos negros son los números enteros ordinarios que se muestran en un plano complejo. La suma o multiplicación de cualquier par de puntos negros termina con otro punto negro. Todos los puntos rojos y azules de esta figura son soluciones a algunas ecuaciones cuadráticas con coeficientes enteros. Los puntos morados son soluciones a algunas ecuaciones cuárticas con coeficientes enteros. Entonces, también podemos pensar en esos puntos como parte de "números". Las operaciones de suma y multiplicación entre puntos negros o rojos permanecen dentro de los "números" mostrados en puntos negros o rojos, y de manera similar, esas operaciones de puntos negros-rojos-azules-morados permanecen dentro de los "números" en puntos negros-rojos-azules-morados. De este modo, es posible expandir el conjunto de "números" integrales gradualmente. Crédito:Kavli IPMU
Una colaboración de un matemático y un físico ha demostrado que las formas modulares asociadas con las curvas elípticas con multiplicaciones complejas se expresan en términos de observables en la teoría de supercuerdas.
El concepto de números puede extenderse desde los números enteros y los números racionales para incluir todos los números reales y complejos, de repente. Pero también es posible ampliar el concepto gradualmente, sumando las raíces de polinomios con coeficientes de números racionales (como la raíz cuadrada de 2 y la raíz cuadrada de 3) poco a poco (Figura 1). Esta clase especial de números complejos se conoce como "números". Los detalles precisos de cómo se puede extender el concepto de números se han considerado como uno de los temas importantes en la teoría de números.
Durante varias décadas, los investigadores han intentado abordar y comprender este problema. Se podría especificar un objeto geométrico mediante ecuaciones utilizando primero los "números", y luego considere el conjunto de puntos en el objeto geométrico cuyos valores son los "números". A medida que el concepto de números se amplía gradualmente, y el conjunto de "números" ampliado, cada vez se cuentan más puntos en el objeto geométrico (Figura 2). La idea es que la forma en que aumenta el número de puntos en el objeto geométrico arrojará luz sobre cómo se expande el conjunto de "números". Es más, esta información de la tasa de crecimiento del número de puntos en el objeto geométrico se empaqueta en una función llamada transformada de Mellin inversa de la función L, que es una función que contiene la información de qué tan rápido crece el número de puntos en un objeto geométrico a medida que se amplía el concepto de números. Se esperaba que esta función fuera una forma modular, una función que permanece invariante bajo ciertas operaciones. Esta conjetura se conoce como conjetura de Langlands.
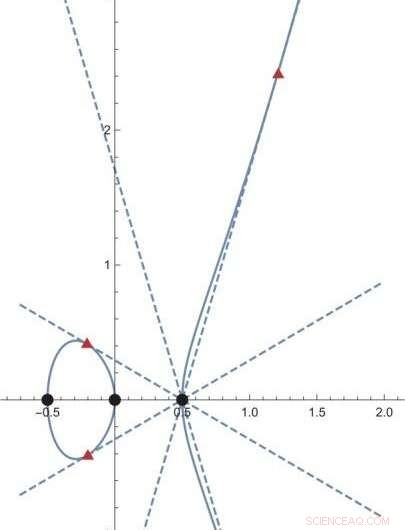
Figura 2. Un objeto geométrico dado por y ^ 2 =4 x ^ 3 - x se muestra mediante una delgada curva azul. En este objeto, los tres puntos negros tienen sus valores en enteros ordinarios. Por otra parte, los tres puntos en triángulos rojos tienen sus valores en un conjunto más expandido de "números" (las coordenadas x son de la forma (p + q sqrt {2}) con números racionales pyq; las coordenadas y son más complicadas) . A medida que se amplía el concepto de "números", aumenta el número de puntos con sus valores en los "números", incluso para un objeto geométrico dado. Crédito:Kavli IPMU
El profesor asociado y teórico de partículas Taizan Watari e investigador de geometría aritmética en el campus de Chipre del Norte de la Universidad Técnica de Oriente Medio del Instituto Kavli de Física y Matemáticas del Universo (Kavli IPMU) y el científico visitante de Kavli IPMU, Satoshi Kondo, se atrevieron a preguntar por qué tales funciones son invariantes bajo ciertas condiciones. operaciones.
En teoría de cuerdas, se sabe que una clase de observables (a) son invariantes bajo las operaciones (x) a las que ya se ha hecho referencia. La invariancia bajo las operaciones es una propiedad indispensable en la construcción teórica de la teoría de supercuerdas. Entonces, los investigadores demostraron que las transformadas inversas de Mellin de las funciones L de los objetos geométricos (b) se expresan en términos de la clase anterior de observables (a) en la teoría de supercuerdas con esos objetos geométricos establecidos como espacios objetivo. Como resultado, se deduce que las funciones que contienen la información de cómo se amplía el concepto de números, las transformaciones inversas de Mellin, (b) debe ser invariante bajo ciertas operaciones, que deben ser formas modulares, (x) por razones desde la perspectiva de la teoría de supercuerdas.
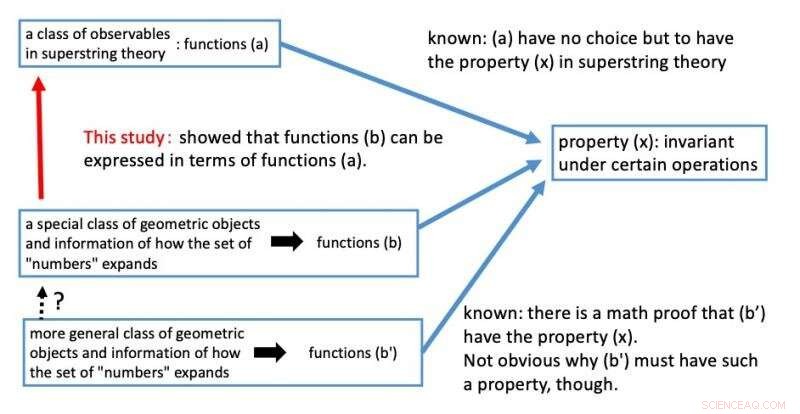
Figura 3. Resumen de este estudio. Crédito:Kavli IPMU
Cabe señalar que el resultado anterior se obtiene solo para la clase de objetos geométricos llamados curvas elípticas con multiplicaciones complejas. Queda abierta la cuestión de si las funciones para una clase más general de objetos geométricos (b) se expresan en términos de observables en la teoría de supercuerdas (a).
Los detalles de este estudio se publicaron el 22 de febrero de 2019, en Comunicaciones en física matemática .