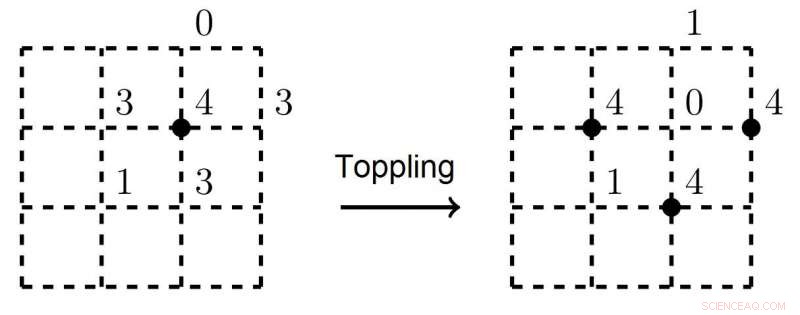
El punto negro de la figura de la izquierda marca un vértice inestable. Después de una avalancha tres vértices vecinos se vuelven inestables y colapsarán Crédito:Nikita Kalinin, Escuela Superior de Economía - San Petersburgo
Un grupo internacional de investigadores (el primer autor es Nikita Kalinin, Escuela Superior de Economía — San Petersburgo, el último autor es Ernesto Lupercio, CINVESTAV, México) ha presentado el primer modelo continuo que describe la criticidad autoorganizada. La solución propuesta es más simple y universal que el modelo clásico de pilas de arena. Integra áreas tan alejadas entre sí como la economía, Biología del desarrollo, y gravedad en el contexto de la geometría tropical. El artículo fue publicado en procedimientos de la Academia Nacional de Ciencias .
Se dice que un sistema está en un estado crítico si una fuerza externa, sin embargo pequeño, puede producir un efecto de avalancha provocando un cambio en el comportamiento del sistema. Estos incluyen transiciones de fase:una vez que un solo cristal de hielo emerge en agua enfriada a cero grados Celsius, un grupo de hielo comenzará a formarse inmediatamente.
Hay ciertos sistemas dinámicos que tienden hacia un estado crítico; los terremotos son un ejemplo ilustrativo. Si bien se requiere una cierta temperatura y presión para que el agua se congele, no es necesario cumplir con parámetros precisos para que ocurra un terremoto. La principal causa de los terremotos es el movimiento continuo de las placas tectónicas, y predecir el momento exacto en que el sistema alcanzará un estado crítico y producirá una avalancha es prácticamente imposible.
Muchos investigadores han intentado resolver el misterio de los terremotos. A mediados del siglo XX, Los sismólogos estadounidenses Gutenberg y Richter mostraron una relación entre la magnitud y el número total de terremotos en una región determinada. Esta relación se describe mediante la ley de potencia expresada como una línea recta en una escala logarítmica doble.
Fenómenos que comparten esta característica se han encontrado desde entonces en geofísica, cosmología, ciencias económicas, teoría de la gestión de riesgos y otros campos. Todos ellos pueden describirse mediante la teoría de la criticidad autoorganizada (SOC).
El concepto de SOC fue introducido por Per Bak, Chao Tang y Kurt Wiesenfeld en 1987. En su artículo fundamental, presentan el ejemplo arquetípico de un sistema SOC:el modelo Sandpile. Imagina una cuadrícula con granos de arena en cada uno de sus vértices, en el que nuevos granos caen en la red a una cierta frecuencia. Se supone que si no hay más de tres granos de arena en cada vértice, el sistema permanecerá estable. Pero tan pronto como un cuarto grano de arena cae sobre un vértice, se derrumba, y la arena se desliza por este pico y se redistribuye a los vértices vecinos. El derrumbe continuará en avalancha hasta que el sistema regrese al equilibrio. El descubrimiento clave de los físicos fue que la cantidad de vértices que se derrumban (es decir, el tamaño de la región colapsada) satisface una distribución de ley de potencias.
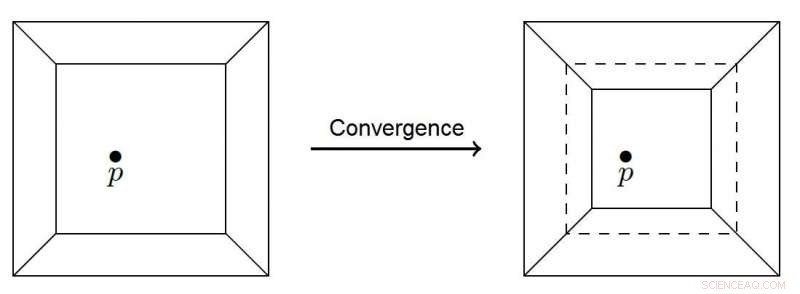
Polígono convergiendo a un punto. Crédito:Nikita Kalinin, Escuela Superior de Economía - San Petersburgo
El modelo de pilas de arena ha sido durante mucho tiempo el modelo clásico que describe el SOC. Sin embargo, describe la dinámica de los sistemas críticos solo a nivel fenomenológico y no puede usarse para simular un terremoto o predecir el comportamiento de un montículo de arena real.
"El viejo modelo de pila de arena, siendo puramente combinacional, se distingue un poco del gran mundo de las matemáticas. Nuestro modelo es un paso adelante, porque tiene todas las ventajas del modelo de pila de arena, pero también es geométrico y continuo, haciéndolo mucho más fácil de usar, "explica la autora Nikita Kalinin, investigador senior del Laboratorio Internacional de Teoría de Juegos y Toma de Decisiones de HSE. "Hemos demostrado que las correlaciones de la ley de potencias se pueden obtener en un sistema continuo que no es un autómata celular con la ayuda de la geometría tropical, que tiene muchas aplicaciones en la actualidad ".
"La geometría tropical es una rama de la geometría del siglo XXI inspirada en la geometría algebraica clásica que ha florecido debido a sus conexiones con muchos campos de la ciencia, principalmente la teoría de cuerdas, "dice el Dr. Ernesto Lupercio del CINVESTAV.
En lugar de la cuadrícula utilizada en el modelo clásico de pilas de arena, el nuevo modelo de pilas de arena tropical considera una curva tropical, un gráfico plano con bordes rectilíneos, encerrado en un cuadrado. La curva divide el cuadrado en regiones poligonales, cada uno contiene un conjunto de puntos elegidos al azar. Cuando se agrega un nuevo punto, la curva tropical intenta atravesarlo, y la región poligonal que contiene el punto se junta mediante una transferencia paralela de sus bordes. Tan pronto como uno de los bordes toque el punto, el proceso se detiene. Luego se agrega un nuevo punto, y comienza todo de nuevo. El punto anterior puede volver a estar fuera de la curva, y el sistema comenzará a moverse hacia él.
Este proceso de convergencia es una variante finita de agregar granos de arena a una pila de arena. En el nuevo modelo, el tamaño de la avalancha corresponde al área barrida por las regiones convergentes en el proceso iniciado al agregar un punto aleatorio. Los científicos esperan que su modelo ayude a aclarar las relaciones entre los diferentes fenómenos que manifiestan las propiedades del COS.
"Podemos observar similitudes en diferentes fenómenos vistos a través de la lente de las matemáticas. La geometría tropical tiene aplicaciones en la teoría de cuerdas, economía y biología del desarrollo. El valor de nuestro trabajo radica en encontrar conexiones en lugares inesperados. Significa que los métodos aplicados a un área se pueden aplicar a otra. Solo necesitas dar el siguiente paso, "dice Kalinin.