
Tarski demostró que un círculo con un radio de uno no puede cubrirse completamente con tiras cuyo ancho combinado es menor que dos:el diámetro del círculo. Cada una de las tiras de la imagen tiene su propia longitud y color. Crédito:MIPT
El Instituto de Tecnología de Israel y Alexandr Polyanskii del Instituto de Física y Tecnología de Moscú (MIPT) han demostrado la conjetura de la zona de László Fejes Tóth. Formulado en 1973, dice que si una esfera unitaria está completamente cubierta por varias zonas, su ancho combinado es al menos π. La prueba, publicado en la revista Análisis geométrico y funcional , es importante para la geometría discreta y permite a los matemáticos formular nuevos problemas.
La geometría discreta estudia las propiedades combinatorias de los puntos, líneas, círculos polígonos y otros objetos geométricos. ¿Cuál es la mayor cantidad de bolas del mismo tamaño que pueden caber alrededor de otra bola del mismo tamaño? ¿Cuál es la forma más densa de empaquetar círculos del mismo tamaño en un plano? o bolas en un espacio contenedor? Estas y otras preguntas se abordan mediante geometría discreta.
Las soluciones a problemas como estos tienen aplicaciones prácticas. Por lo tanto, El denso problema del empaque ha ayudado a optimizar la codificación y corregir errores en la transmisión de datos. Otro ejemplo es el teorema de los cuatro colores, que dice que cuatro colores son suficientes para trazar cualquier mapa en una esfera de modo que no haya dos regiones adyacentes con el mismo color. Ha llevado a los matemáticos a introducir conceptos importantes para la teoría de grafos, que es crucial para muchos de los desarrollos recientes en química, biología e informática, así como sistemas logísticos.
La conjetura de la zona de Tóth está estrechamente relacionada con una serie de otros problemas de geometría discreta que se resolvieron en el siglo XX al tratar de cubrir una superficie con tiras. El primero de ellos fue el llamado problema de las planchas, lo que implicaba cubrir un disco con tiras delimitadas por líneas paralelas. Alfred Tarski y Henryk Moese ofrecieron una prueba simple que muestra que el ancho combinado de estas tiras, o tablones, no puede exceder el diámetro del disco. Es decir, No hay mejor manera de cubrir un disco que con una sola tabla cuyo ancho sea igual al diámetro del disco. Thøger Bang luego resolvió el problema de cubrir un cuerpo convexo arbitrario con tiras. A saber, demostró que el ancho combinado de las tiras que cubren un cuerpo convexo es al menos el ancho del cuerpo mismo, es decir, el ancho mínimo de una sola tira que cubre el cuerpo.
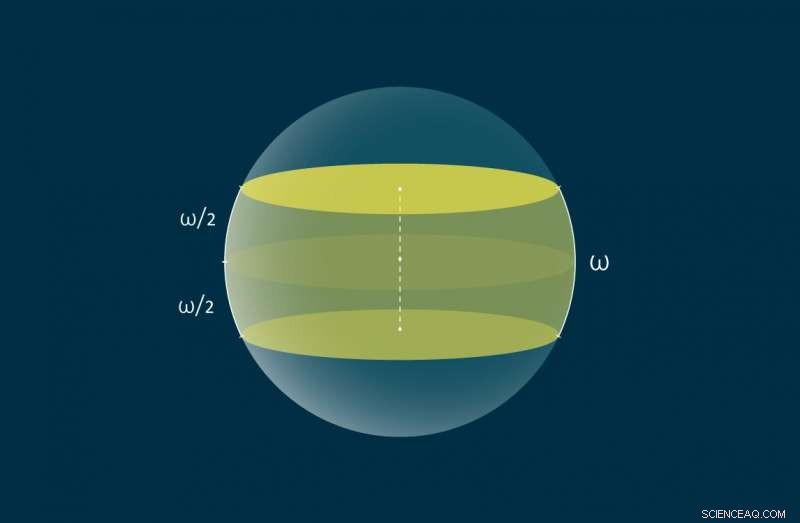
Una zona de ancho ω en la esfera se muestra en amarillo. Crédito:MIPT
El problema abordado por los autores es diferente en el sentido de que se trata de cubrir una esfera unitaria con zonas especialmente construidas. Específicamente, cada zona es la intersección de la esfera con una determinada tabla tridimensional, donde una tabla es la región del espacio contenida entre dos planos paralelos que son simétricos con respecto al centro de la esfera. Alternativamente, Las zonas se pueden definir en el espacio métrico geodésico sin recurrir a tablones:Una zona de ancho ω en la superficie de una esfera unitaria es el conjunto de puntos que se encuentran a no más de ω / 2 del gran círculo, o ecuador, con las distancias entre los puntos medidos como los arcos más cortos que los conectan. Los matemáticos tuvieron que encontrar el ancho mínimo combinado de tales zonas que cubren la esfera unitaria. Por lo tanto, el problema difiere de los previamente resueltos en cómo se mide el ancho:se define como la longitud de un arco, en lugar de la distancia euclidiana entre líneas o planos paralelos.
La prueba presentada por Jiang y Polyanskii se inspiró en Bang, que resolvió el problema de cubrir un cuerpo con tiras formando un conjunto finito especial de puntos dentro del cuerpo, uno de los cuales supuestamente no estaba cubierto por ninguna de las tiras. En cierto sentido, tanto Bang como los autores producen una prueba por contradicción. En el caso de la conjetura de Fejes Tóth, los matemáticos plantearon la hipótesis de que el ancho combinado de las zonas que cubrían completamente la esfera era menor que π y buscaron llegar a una contradicción, a saber, encontrar un punto que se encuentre en la esfera pero no en ninguna de las zonas.
Los autores han demostrado que es posible formar un conjunto de puntos en un espacio tridimensional de modo que al menos un punto no quede cubierto por los tablones que constituyen las zonas. Si todo este conjunto se encuentra dentro de la esfera, Entonces es relativamente fácil trazar otro punto en la esfera que tampoco esté cubierto por las tablas, y por tanto por las zonas. Si alguno de los puntos del conjunto queda fuera de la esfera, resulta posible sustituir una zona más grande por varias más pequeñas, cuyo ancho combinado es igual al de la zona mayor. Por lo tanto, es posible reducir el número de zonas en el problema inicial sin afectar su ancho combinado. Finalmente, se identifica un punto de la esfera que no está cubierto por las zonas. Esto contradice la hipótesis de que el ancho combinado de las zonas es menor que π, probando la conjetura de Fejes Tóth.

Zonas que cubren completamente una esfera. Cada una de las cinco zonas tiene su propio ancho y color. Crédito:MIPT
El problema se resolvió en un espacio n-dimensional, pero los autores dicen que esto no lo hace diferente del caso con tres dimensiones.
"El problema de Fejes Tóth ha fascinado a los matemáticos en el campo de la geometría discreta durante más de 40 años, "dice el autor Alexandr Polyanskii del Departamento de Matemáticas Discretas, MIPT. "Este problema resultó tener una solución elegante, que tuvimos la suerte de encontrar. El problema de Fejes Tóth nos llevó a considerar otro, conjetura más fundamental sobre la cobertura de una esfera por zonas desplazadas definidas como la intersección de la esfera con tablas tridimensionales que no son necesariamente simétricas centralmente ".