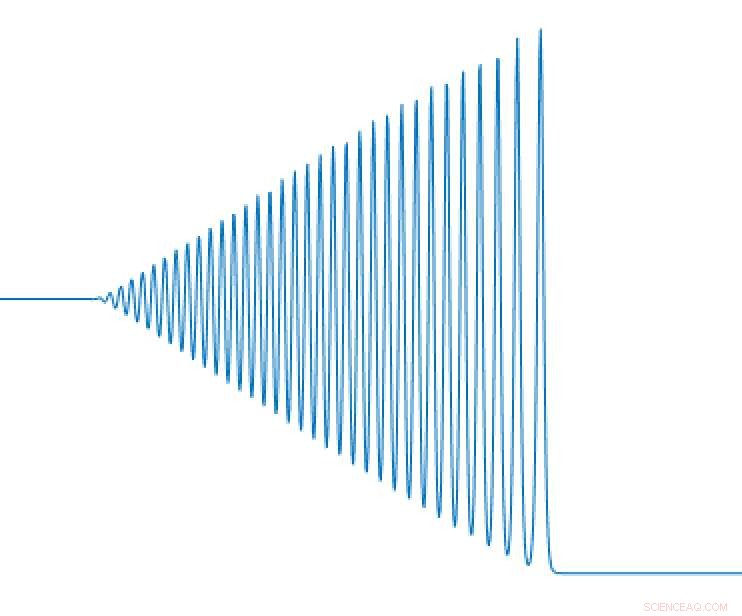
Diagrama esquemático que muestra el perfil típico de la altura del fluido a través de un orificio ondular. Crédito:Qiao Wang
Cuando un fluido o un gas experimenta una alteración repentina, como un cambio de presión o elevación, a menudo da lugar a un fenómeno conocido como un agujero ondular, que consiste en una serie de oscilaciones rápidas que se propagan y difunden.
En naturaleza, este espectáculo ocurre en muchos escenarios diferentes, incluyendo ondas de agua y plasmas, un estado de la materia que consiste en gases ionizados con partículas libres cargadas positiva y negativamente. También ocurren fenómenos similares en la atmósfera.
Pero, ¿cómo describir lo que sucede?
Un nuevo artículo de matemáticos de la Universidad de Buffalo y la Universidad de Colorado Boulder nos acerca a encontrar una respuesta.
La investigación, publicado en agosto en el Actas de la Royal Society A , establece un conjunto de ecuaciones recién formuladas que están diseñadas para caracterizar lo que sucede cuando se produce un taladro ondular y se extiende a lo largo de dos ejes. Visualmente, este fenómeno se asemeja a las ondas concéntricas que proliferan hacia afuera cuando arrojas una piedra a un estanque.
"Ves estos efectos en el agua, en plasmas, en la atmósfera, por lo que las ecuaciones que describen estas ondas surgen en un montón de campos diferentes, "dice Gino Biondini, Doctor, Catedrático de Matemáticas en la Facultad de Artes y Ciencias de la UB. "Nos gusta decir que las matemáticas son universales; las mismas matemáticas te permiten describir muchos escenarios diferentes".
Los socios de Biondini en el estudio fueron Mark J. Ablowitz, Doctor, profesor de matemáticas aplicadas en la Universidad de Colorado Boulder, y Qiao Wang, Candidato a doctorado en matemáticas por la UB.
Un avance en la matemática ondulatoria
En los años 1960, Al matemático Gerald B. Whitham se le ocurrió un enfoque para describir los taladros ondulares. Las ecuaciones que formuló solo podían usarse, sin embargo, cuando una ola viajaba a lo largo de un solo eje (como una marea que se propaga en una dirección por un canal estrecho).
El nuevo artículo de Ablowitz, Biondini y Wang se basan en la teoría de Whitham al derivar un conjunto de ecuaciones diseñadas para describir cómo se forman y propagan tales ondas a lo largo de dos ejes, en dos direcciones posibles.
Dentro de este marco bidimensional, el equipo ya ha utilizado sus ecuaciones para estudiar perforaciones ondulares cuya altura de ola varía a lo largo de solo una de las dos direcciones disponibles. El siguiente paso en la investigación es aplicar las ecuaciones en la caracterización de perforaciones ondulares cuya altura de ola cambia a lo largo de ambos ejes.
"Las ecuaciones que formulamos marcan un paso adelante para describir estos interesantes fenómenos, "Dice Biondini". Además, los métodos que usamos se pueden aplicar para estudiar una variedad de problemas físicos relacionados, por lo que esperamos que nuestros resultados abran una larga serie de trabajos sobre este tipo de temas ".