
Crédito:CC0 Public Domain
Los superconductores topológicos (TSC) son un nuevo tipo de estados cuánticos topológicos con una estructura de banda con huecos completamente superconductores en la mayor parte, pero admiten excitaciones sin espacios llamadas modos cero de Majorana (MZM) en los límites. Debido a su correlación no local y su naturaleza estadística no abeliana, Los MZM se proponen como los qubits de la computación cuántica topológica. Por eso, buscar y operar los MZM en materiales TSC es ahora un tema importante en la física de la materia condensada.
Para identificar un TSC, primero se debe determinar su clasificación topológica. La clasificación topológica depende en gran medida de las simetrías, incluida la simetría de inversión del tiempo, simetría de huecos de partículas, y especialmente las simetrías cristalinas. Sin la consideración de simetrías cristalinas, los hamiltonianos Bogoliubov-deGennes (BdG) de los superconductores 1-D solo tienen la clasificación Z2. La simetría de reflexión de espejo y las simetrías rotacionales pueden mejorar la clasificación a la clase Z. Sin embargo, la clasificación topológica de superconductores con simetrías magnéticas generales sigue siendo una cuestión abierta.
En un nuevo artículo de investigación publicado en Beijing, Revista Nacional de Ciencias , científicos de la Universidad de Ciencia y Tecnología de Huazhong en Wuhan, Porcelana, y la Universidad de Princeton en Nueva Jersey, EE.UU. propuso el método para clasificar la fase superconductora topológica examinando la compatibilidad entre diferentes MZM. Coautores Jinyu Zou, Qing Xie, Zhida Song y Gang Xu analizaron la clasificación topológica de cables superconductores con huecos con simetrías magnéticas locales (LMS). Descubrieron que se puede realizar un TSC de clase BDI eficaz en M X T o C 2z T alambre invariante. Notablemente, las nuevas fases TSC caracterizadas por Zh invariante en C 4z Se descubre el caso T y el invariante Zhoplus Zc en el caso C6zT.
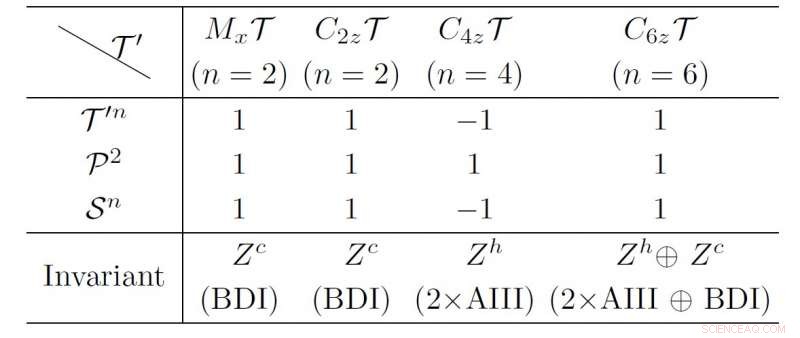
La clasificación topológica de los sistemas superconductores con huecos 1D con los LMS. Crédito:© Science China Press
En el artículo titulado "Nuevos tipos de superconductores topológicos bajo simetrías magnéticas locales". Los autores se centran en los cables superconductores 1D con LMS T '=M X T, C 2z T, C 4z T y C 6z T. "La operación de T 'no cambia la posición de los electrones. Por lo tanto, actúa sobre el Hamiltoniano BdG como un operador de inversión de tiempo". La combinación de la simetría P 'y la partícula-agujero conduce a una simetría quiral S =T'P. El Hamiltoniano BdG puede adoptar la forma diagonalizada de acuerdo con la simetría quiral. Y los MZM son los estados propios de la simetría quiral S. Los autores encuentran que "los MZM que tienen valores propios quirales sy -s pueden acoplarse entre sí y eliminarse". Siguiendo la directriz, Analizan la compatibilidad de los MZM al final de los cables superconductores 1D con los LMS, y resumir su clasificación topológica como se enumera en la Tabla I.
Ellos X T y C 2z Los casos T son equivalentes a la clase BDI con invariante topológico quiral Zc. Mientras que el caso C4zT se caracteriza por una Z helicoidal h invariante, que indican múltiples pares de Majorana Kramer al final del cable superconductor. En la C 6z Caso T, "la topología de todo el Hamiltoniano BdG se clasifica mediante Z h oplus Z C , ". En una fase topológica tan novedosa, "Los MZM helicoidales y quirales pueden coexistir".
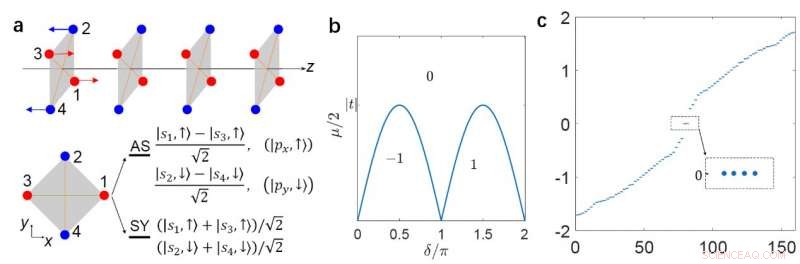
(a) Un cable superconductor que conserva C4zT alineado a lo largo de la dirección z. (b) El diagrama de fase topológico. (c) el espectro de fase no trivial con un límite abierto en ambos lados, en el que aparecen cuatro MZM con energía cero. Crédito:© Science China Press
"Para ilustrar la fase TSC con el LMS C 4z T, construimos una cadena anti-ferromagnética 1D a lo largo de la dirección z, "añaden los científicos. Dan el diagrama de fase topológica del modelo". En la fase TSC no trivial, el cable cuántico abierto atrapa un par entero de MZM en sus extremos ". También muestran los MZM a través de cálculos numéricos y analíticos.
"Estos resultados no solo enriquecen la variedad del 1-D TSC, pero también proporcionan bloques de construcción exuberantes para la construcción de nuevos TSC de tipo 2-D y 3-D ", pronostican al final del artículo, "Por ejemplo, se pueden acoplar los TSC 1D en la dirección y para construir un TSC 2-D. Las líneas de alta simetría ky =0 y ky =pi en el espacio de momento conservan el LMS 1D. Con los parámetros adecuados, las líneas ky =0 y ky =pi pueden pertenecer a distintas fases topológicas, y dan como resultado los estados de borde de Majorana que se propagan sin espacios que conectan las bandas conductoras y las bandas de valencia ".