
Los procesos de Markov se han utilizado para modelar la acumulación de pilas de arena. Crédito:Prensa del Instituto Santa Fe
Los científicos creen que el tiempo es continuo, no discreto, en términos generales, creen que no progresa en "trozos, "sino que" fluye, "sin problemas y de forma continua. Por lo tanto, a menudo modelan la dinámica de los sistemas físicos como procesos de Markov de tiempo continuo, "nombrado en honor al matemático Andrey Markov. De hecho, Los científicos han utilizado estos procesos para investigar una variedad de procesos del mundo real desde el plegamiento de proteínas, a los ecosistemas en evolución, a los mercados financieros cambiantes, con asombroso éxito.
Sin embargo, invariablemente, un científico solo puede observar el estado de un sistema en momentos discretos, separados por alguna brecha, en lugar de continuamente. Por ejemplo, un analista del mercado de valores podría observar repetidamente cómo el estado del mercado al comienzo de un día se relaciona con el estado del mercado al comienzo del día siguiente, construir una distribución de probabilidad condicional de lo que se le da al estado del segundo día al estado del primer día.
En un par de papeles uno que aparece en el de esta semana Comunicaciones de la naturaleza y uno que apareció recientemente en el Nueva Revista de Física , Los físicos del Instituto Santa Fe y del MIT han demostrado que para que esa dinámica de dos tiempos sobre un conjunto de "estados visibles" surja de un proceso de Markov de tiempo continuo, que el proceso de Markov debe desarrollarse en un espacio más grande, uno que incluye estados ocultos además de los visibles. Además, demuestran que la evolución entre ese par de tiempos debe proceder en un número finito de "pasos de tiempo ocultos", subdividiendo el intervalo entre esos dos tiempos. (Estrictamente hablando, esta prueba es válida siempre que la evolución desde el momento anterior al posterior sea libre de ruidos; consulte el documento para obtener detalles técnicos).
"Estamos diciendo que hay variables ocultas en los sistemas dinámicos, implícito en las herramientas que los científicos están usando para estudiar tales sistemas, "dice el coautor David Wolpert (Instituto Santa Fe)". Además, en cierto sentido muy limitado, estamos diciendo que el tiempo transcurre en pasos de tiempo discretos, incluso si el científico modela el tiempo como si avanzara continuamente. Es posible que los científicos no hayan estado prestando atención a esas variables ocultas y esos pasos de tiempo ocultos, pero están ahí, tocando una tecla, papel detrás de escena en muchos de los artículos que esos científicos han leído, y casi con seguridad también en muchos de los artículos que esos científicos han escrito ".
Además de descubrir estados ocultos y pasos de tiempo, los científicos también descubrieron una compensación entre los dos; los estados más ocultos hay, cuanto menor sea el número mínimo de pasos de tiempo ocultos que se requieren. Según el coautor Artemy Kolchinsky (Instituto Santa Fe), "Estos resultados demuestran sorprendentemente que los procesos de Markov exhiben una especie de compensación entre el tiempo y la memoria, que se encuentra a menudo en el campo matemático separado del análisis de algoritmos informáticos.
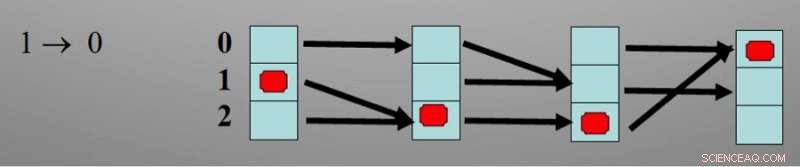
La configuración mínima para cambiar un poco de información de 1 a 0 requiere tres estados y tres pasos de tiempo secuenciales. Crédito:David Wolpert
Para ilustrar el papel de estos estados ocultos, el coautor Jeremy A. Owen (MIT) da el ejemplo de un proceso biomolecular, observado a intervalos de una hora:si comienza con una proteína en el estado 'a, 'y más de una hora generalmente cambia al estado' b, 'y luego de otra hora por lo general vuelve a' a, 'debe haber al menos otro estado' c ', un estado oculto, que esté influyendo en la dinámica de la proteína. "Está ahí en su proceso biomolecular, ", dice." Si aún no lo ha visto, puedes ir a buscarlo ".
Los autores tropezaron con la necesidad de estados ocultos y pasos de tiempo ocultos mientras buscaban la forma más eficiente desde el punto de vista energético para voltear un poco de información en una computadora. En esa investigación, parte de un esfuerzo mayor para comprender la termodinámica de la computación, descubrieron que no existe una forma directa de implementar un mapa que envíe 1 a 0 y también envíe 0 a 1. Más bien, para voltear un poco de información, el bit debe pasar por al menos un estado oculto, e implican al menos tres pasos de tiempo ocultos. (Ver diagrama adjunto multimedia)
Resulta que cualquier sistema biológico o físico que "calcula" las salidas de las entradas, como una célula que procesa energía, o un ecosistema en evolución, ocultaría las mismas variables ocultas que en el ejemplo de inversión de bits.
"Este tipo de modelos realmente surgen de forma natural, "Owen agrega, "basado en los supuestos de que el tiempo es continuo, y que el estado en el que te encuentras determina a dónde vas a ir a continuación ".
"Una cosa que fue sorprendente, que hace que esto sea más general y más sorprendente para nosotros, fue que todos estos resultados se mantienen incluso sin consideraciones termodinámicas, "Wolpert recuerda." Es un ejemplo muy puro del mantra de Phil Anderson 'más es diferente, 'porque todos estos detalles de bajo nivel [estados ocultos y pasos de tiempo ocultos] son invisibles para los detalles de nivel superior [mapa del estado de entrada visible al estado de salida visible] ".
"De una manera muy menor, es como el límite de la velocidad de la luz, "Wolpert reflexiona, "El hecho de que los sistemas no puedan exceder la velocidad de la luz no es una consecuencia inmediata para la gran mayoría de los científicos. Pero es una restricción en los procesos permitidos que se aplica en todas partes y es algo que siempre debe tener en cuenta".