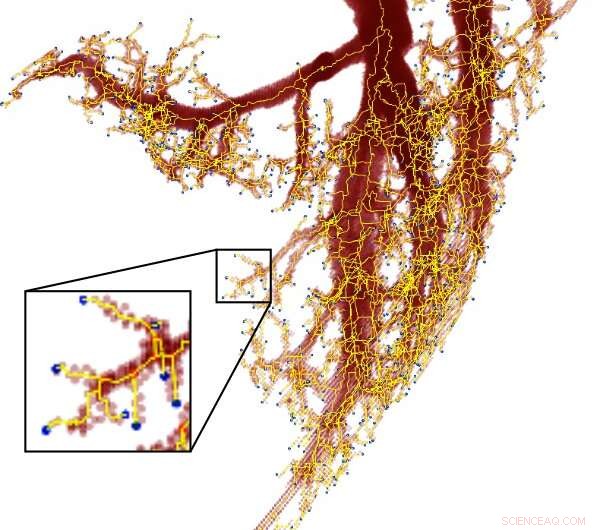
Debido a que las venas se ramifican en divisiones aproximadamente proporcionadas, también se consideran fractales. Crédito:Imagen de cortesía / Mitchell Newberry
Los terremotos gigantes y la riqueza extrema pueden no parecer tener mucho en común, pero la frecuencia con la que el "Big One" llegará a San Francisco y la frecuencia con la que alguien ganará tanto dinero como Bill Gates pueden predecirse con una medida estadística llamada exponente de la ley de potencia.
Durante el último siglo, Los investigadores han utilizado lo que se llama una ley de potencia para predecir ciertos tipos de eventos, incluida la frecuencia con la que ocurrirán terremotos en ciertos puntos de la escala de Richter. Pero un investigador de la Universidad de Michigan notó que esta ley de poder no se ajusta a todas las circunstancias.
Mitchell Newberry, un miembro de Michigan y profesor asistente en el Centro de la U-M para el Estudio de Sistemas Complejos, sugiere un ajuste a la ley de potencia que daría cuenta de eventos que aumentan o disminuyen en proporciones fijas, por ejemplo, cuando un gerente gana aproximadamente un 20 por ciento más que su empleado.
Estos ajustes afectan la forma de estimar las probabilidades de terremotos, la cantidad de capilares en el cuerpo humano, y el tamaño de las megaciudades y las erupciones solares. Y pueden revisar cuándo esperar el próximo Big One.
Cuando los científicos trazan algo como la probabilidad de riqueza extrema en un gráfico, la curva es una línea suave. Eso es porque las personas pueden tener cualquier cantidad de dinero en sus cuentas bancarias.
"La suavidad de esta curva significa que cualquier valor es posible, ", Dijo Newberry." Podría ganar un centavo más con la misma facilidad que un centavo menos ".
Ese no es exactamente el caso de eventos como terremotos debido a cómo se registran en la escala de Richter. La magnitud de Richter de los terremotos aumenta o disminuye en incrementos de 0.1, exponencialmente. Un terremoto de magnitud 3,1 es 1,26 veces más poderoso que un terremoto de magnitud 3,0, por lo que no todos los valores son posibles en la escala. La escala de Richter es un ejemplo de un concepto llamado "auto-semejanza, "o cuando un evento o cosa está hecha de copias proporcionalmente más pequeñas de sí mismo.
Puedes ver la auto-semejanza en la naturaleza como la ramificación de las venas en una hoja, o en geometría como encajar triángulos dentro de triángulos más grandes de la misma forma, llamado triángulo de Sierpinski. Entonces, para dar cuenta de los eventos que cambian en proporciones exactas, Newberry y su coautor Van Savage de la Universidad de California, Los Angeles, construyó la ley de potencia discreta.

La curva de Koch se repite infinitamente, mostrando auto-semejanza. Crédito:usuario de Wikimedia Leofun01
En estas ecuaciones de la ley de potencias, el exponente de la ecuación es la variable que los científicos están resolviendo. En terremotos ese exponente, llamado valor b de Gutenberg-Richter, se midió por primera vez en 1944 e indica la frecuencia con la que es probable que ocurra un terremoto de cierta intensidad. La ley de potencia discreta de Newberry produjo una corrección del 11,7% sobre las estimaciones basadas en la ley de potencia continua, acercando el exponente a la frecuencia histórica de grandes terremotos. Incluso una corrección del 5% se traduce en una diferencia de más del doble en cuanto a cuándo esperar el próximo terremoto gigante.
"Durante 100 años, la gente ha estado hablando aproximadamente de un tipo de distribución de la ley de potencia. Es la distribución de la ley de poder de la riqueza y los terremotos, ", Dijo Newberry." Sólo ahora, estamos documentando estas escalas discretas. En lugar de una curva suave, nuestra ley de potencia parece una escalera infinita ".
Newberry notó la falla en la ley de potencia continua en su estudio de la física del sistema circulatorio. El sistema circulatorio comienza con un vaso sanguíneo grande:la aorta. A medida que la aorta se divide en diferentes ramas, las arterias carótida y subclavia, cada nueva rama disminuye de diámetro en aproximadamente dos tercios.
Estaba usando la ley de potencia continua para estimar el tamaño de los vasos sanguíneos a medida que continúan ramificándose. Pero la ley de potencia produjo tamaños de vasos sanguíneos que no podían ocurrir. Indicó que un vaso sanguíneo podría ser solo un poco más pequeño que el tronco del que se ramifica en lugar de alrededor de dos tercios del tamaño de ese tronco.
"Utilizando la ley de potencia continua, solo estábamos obteniendo respuestas que sabíamos que estaban mal ", Dijo Newberry." Al depurar lo que falló, Descubrimos que esta distribución supone que todos los tamaños de vasos sanguíneos son igualmente plausibles. Sabemos que para la vasculatura real, ese no es el caso."
Así que Newberry hizo ingeniería inversa a la ley de potencia. Al observar los vasos sanguíneos, Newberry podría deducir el exponente de la ley de potencia a partir de dos constantes:cuántas ramas en cada unión (dos) y cuánto más pequeña es cada rama en relación con el tronco. Medir el tamaño de los recipientes en cada división, Newberry pudo resolver la distribución de los vasos sanguíneos.
"Hay un término medio entre una ley de potencia continua y la ley de potencia discreta, ", Dijo Newberry." En la ley de potencia discreta, todo está dispuesto en proporciones perfectamente rígidas desde la escala más alta hasta la infinitesimalmente pequeña. En la ley de potencia continua, todo está perfectamente distribuido al azar. Casi todo lo que se asemeja a sí mismo en realidad es una mezcla de estos dos ".
El estudio de Newberry se publica en la revista Cartas de revisión física .