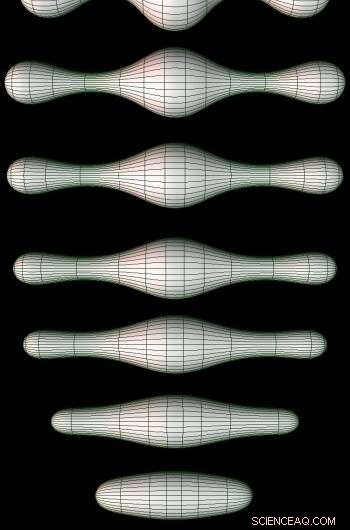
Las etapas servales de Ricci Flow en una variedad 2D. Crédito:https://en.wikipedia.org/wiki/Ricci_flow
La geometría diferencial es el estudio de la geometría espacial. Múltiples fenómenos naturales, desde la expansión universal hasta la expansión y contracción térmica, puede reducirse a la evolución espacial. Las dos conjeturas centrales en este campo, la conjetura de Hamilton-Tian y la C parcial 0 conjetura, fueron rompecabezas sin resolver durante más de 20 años.
"La mayoría de los guijarros de la playa son redondos. Es posible que al principio tuvieran bordes y esquinas, pero a medida que pasa el tiempo y la marea baja y baja, su forma se acercará cada vez más a la perfección y al estándar. Pero no importa cuán perfecta sea la evolución, todavía puede haber algunas anomalías, que se llaman 'singularidades' en geometría ".
"La conjetura de Hamilton-Tian sugiere que la mayor parte del espacio es perfecto, mientras que el tamaño de la 'singularidad' puede restringirse a un espacio de baja dimensión, "dijo el profesor Chen Xiuxiong, el fundador del Instituto de Geometría y Física, Universidad de Ciencia y Tecnología de China (USTC) de la Academia de Ciencias de China (CAS).
Profesor Chen, junto con el profesor Wang Bing de la USTC, Primero demostró las dos conjeturas.
Su artículo se dividió en 123 páginas en dos partes de, el primero de los cuales se publicó en 2017 y el segundo este año en Revista de geometría diferencial , que también publicó el trabajo fundamental de Hamilton sobre el flujo de Ricci después de un largo curso de cinco años de desarrollo de la teoría y seis años de revisión por pares desde su primera presentación.
Este trabajo enfatizó la teoría de la compacidad débil para los flujos de Ricci no colapsados. Introdujo muchos pensamientos y métodos innovadores, que aportaron implicaciones de gran alcance en el campo del análisis geométrico, especialmente para los estudios de los flujos de Ricci.
De hecho, Se han desarrollado muchos otros trabajos basados en este artículo. Por ejemplo, El profesor Chen dio una nueva solución para la estabilidad de la conjetura de Yau basada en la teoría de la estructura de los flujos de Ricci. El Prof. Wang y el Dr. Sun Song de la USTC con su derivación publicada en Geometría y topología . Antes de que, recibieron el Premio Oswald Veblen en Geometría por la primera solución de la estabilidad de la conjetura de Yau.
La teoría y los métodos presentados en este artículo también se aplicaron en una serie de trabajos del Prof. Wang y sus colaboradores en los últimos años.
Las ideas centrales de este artículo se generalizaron a la investigación del flujo de curvatura media por el profesor Wang y el profesor Li Haozhao, quién resolvió el problema de la extensión, y el resultado se publicó en Inventos Mathematicae .
El documento del Prof. Wang, Dr. Huang Shaosai y Dr. Li Yu, "Sobre la convexidad regular de los espacios límite de Ricci Shrinker, " publicado en Diario de Crelle , ha demostrado que el límite de los solitones de Ricci que se contraen no colapsados debe ser la forma de cono definida por el Prof. Chen y el Prof. Wang.
Adicionalmente, el artículo "Heat Kernel on Ricci Shrinkers, " publicado en Cálculo de variaciones y ecuaciones diferenciales parciales por el Prof. Wang y el Dr. Li, desarrolló varias estimaciones a través del estudio del núcleo de calor en encogidores de Ricci y proporcionó "herramientas necesarias para analizar las singularidades de corto tiempo de los flujos de Ricci de dimensión general".
Este avance fue honrado por el revisor de la revista y el ganador de Fields Metal, Prof. Simon Donaldson, quien dijo, "este trabajo es un gran avance en el análisis geométrico, y sin duda liderará muchos otros proyectos de investigación relacionados ".