
Ejemplo de una sección transversal de la superficie K3 en 3 espacios, similar a un modelo de la Universidad Estatal de Utah y la Universidad de Missouri-St. Los matemáticos de Louis solían examinar las dualidades de cuerdas entre la teoría F y la teoría heterótica en ocho dimensiones. Crédito:USU
Simplemente pon, la teoría de cuerdas es un método propuesto para explicar todo. Realmente, no tiene nada de simple. La teoría de cuerdas es un marco teórico de la física que describe unidimensional, objetos fibrosos vibrantes llamados "cuerdas, "que se propagan por el espacio e interactúan entre sí. Pieza a pieza, las mentes enérgicas están descubriendo y descifrando las cadenas fundamentales del universo físico utilizando modelos matemáticos. Entre estos intrépidos exploradores se encuentran los matemáticos de la Universidad Estatal de Utah Thomas Hill y su mentor de la facultad, Andreas Malmendier.
Con su colega Adrian Clingher de la Universidad de Missouri-St. Luis el equipo publicó hallazgos sobre dos ramas de la teoría de cuerdas en el artículo, "La dualidad entre la teoría F y la cuerda heterótica en D =8 con dos líneas de Wilson, "en el 7 de agosto, Edición en línea 2020 de Letters in Mathematical Physics. El trabajo de los investigadores de la USU cuenta con el apoyo de una subvención de la Fundación Simons.
"Estudiamos una familia especial de superficies K3:compactas, superficies complejas conectadas de dimensión 2, que son herramientas geométricas importantes para comprender las simetrías de las teorías físicas, "dice Hill, quien se graduó del Programa de Honores de la USU con una licenciatura en matemáticas en 2018 y completó una maestría en matemáticas la primavera pasada. "En este caso, estábamos examinando una dualidad de cuerdas entre la teoría F y la teoría de cuerdas heterótica en ocho dimensiones ".
Hill dice que el equipo demostró que las superficies K3 que investigaron admiten cuatro formas únicas de cortar las superficies como fibraciones elípticas jacobianas. formaciones de fibras en forma de toro. Los investigadores construyeron ecuaciones explícitas para cada una de estas fibraciones.
"Una parte importante de esta investigación consiste en identificar ciertos bloques de construcción geométricos, llamados 'divisores, "dentro de cada superficie K3, ", dice." Con estos divisores, la información geométrica crucial se codifica en un gráfico abstracto ".
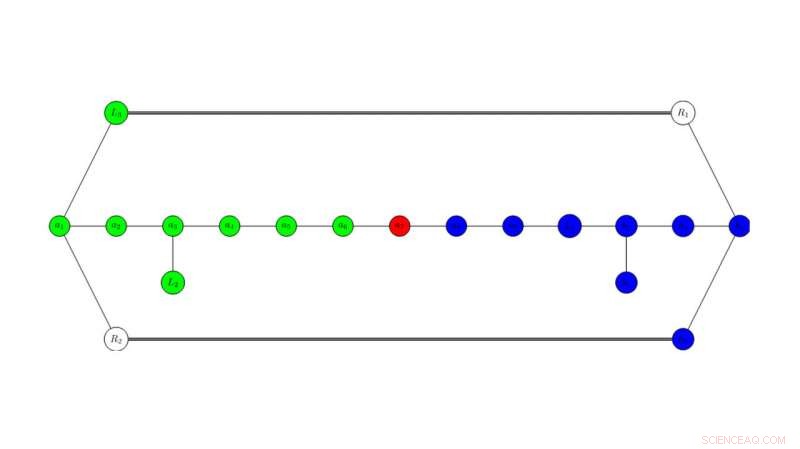
Usando un gráfico abstracto, Los investigadores de la Universidad Estatal de Utah identifican divisores dentro de cada superficie K3 para examinar diversas simetrías. Las diferentes fibraciones elípticas jacobianas corresponden a colores específicos de un subconjunto conectado de los nodos del gráfico. Las simetrías del gráfico y los posibles colores de los nodos son cruciales para comprender las simetrías de las teorías físicas subyacentes. Crédito:Malmendier / Hill, USU
Este proceso, Hill dice:permite a los investigadores investigar las simetrías de las teorías físicas subyacentes demostradas por el gráfico.
"Puedes pensar en esta familia de superficies como una barra de pan y cada fibración como una 'rebanada' de esa barra, "dice Malmendier, profesor asociado en el Departamento de Matemáticas y Estadística de la USU. "Al examinar la secuencia de cortes, podemos visualizar, y entender mejor, todo el pan ".
La empresa descrita en el documento, él dice, representa horas de minucioso trabajo de "lápiz y papel" para demostrar los teoremas de cada una de las cuatro fibraciones, seguido de empujar cada teorema a través de fórmulas algebraicas difíciles.
"Para la última parte de este proceso, utilizamos Maple Software y el paquete especializado de geometría diferencial desarrollado en USU, que agilizó nuestros esfuerzos computacionales, "Dice Malmendier.