Un matemático de la Universidad de la RUDN ha demostrado por primera vez el teorema de existencia y unicidad de las soluciones de la ecuación de Zakharov-Kuznetsov en una tira. Tales teoremas son muy raros para las ecuaciones diferenciales parciales. Los nuevos resultados se pueden aplicar en campos como la astrofísica, por ejemplo, al describir la propagación de ondas planas en plasma. El artículo se publica en la revista Análisis no lineal:aplicaciones del mundo real .

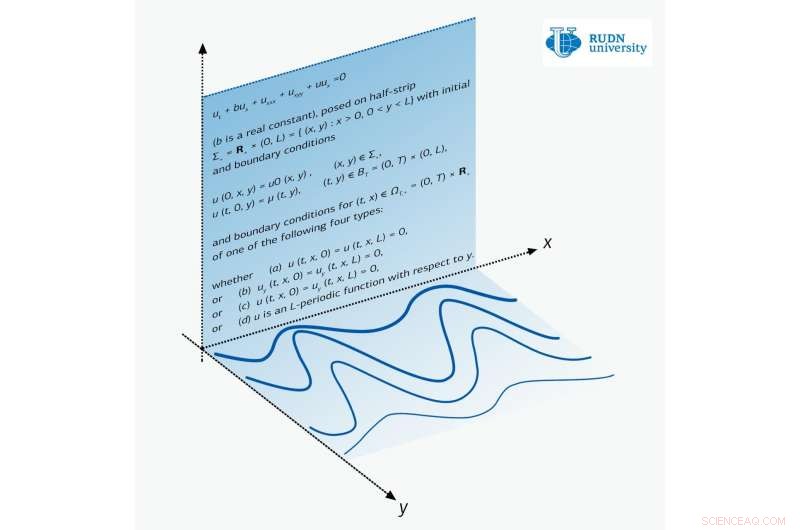
La ecuación de Zakharov-Kuznetsov es una ecuación de una función de dos variables x e y. Para la física, x es la dirección de propagación de la onda, y la deformación del medio se produce a lo largo de la dirección perpendicular y. Por ejemplo, en la oscilación de una cuerda de guitarra, la ola parece correr por la cuerda, mientras que las oscilaciones ocurren perpendicularmente con respecto al recorrido de la ola.

Hay una gran cantidad de resultados que describen soluciones de las ecuaciones de Zakharov-Kuznetsov en el caso en que no hay restricciones en y. Pero la cuestión de la propagación de ondas en la franja, cuando y es limitada, no se estudió ampliamente hasta hace poco.

Los matemáticos de la Universidad RUDN se ocuparon de la ecuación de Zakharov-Kuznetsov en la tira. Examinaron tres casos principales:cuando no hay oscilaciones en el límite de la franja, cuando no hay corriente en el mismo límite, y cuando las condiciones de contorno son de estructura periódica. El último caso corresponde a la propagación de ondas en un medio cuya estructura es periódica en x.

En todos estos casos, los matemáticos lograron probar teoremas de existencia y la unicidad de sus soluciones. Para sistemas de ecuaciones diferenciales parciales, que incluyen la ecuación de Zakharov-Kuznetsov, tales ecuaciones son muy raras.

Estos resultados son los primeros para soluciones de la ecuación con condiciones iniciales en la tira. Flujos de plasma planos con condiciones de contorno, que se encontraban entre los fenómenos considerados por los científicos de la Universidad RUDN, puede ocurrir en física y astrofísica.

Las ecuaciones de Zakharov-Kuznetsov pertenecen a una categoría más amplia de ecuaciones conocidas como ecuaciones de Korteweg-de Vries. En el estudio de esta categoría de ecuaciones, ahora es posible describir los solitones, ondas cuya forma no cambia durante el movimiento. Los físicos consideran los solitones como una herramienta para los sistemas modernos de transmisión de datos ópticos. El estudio de los solitones, que puede surgir en las ecuaciones de Zakharov-Kuznetsov, es una de las opciones para el desarrollo del trabajo realizado por los matemáticos de la Universidad RUDN.