¿Cómo pruebas algo? ¿Qué es la prueba?

En la ciencia, la palabra "prueba" se usa raras veces y con mucho cuidado. Los científicos aceptan que el mundo natural está lleno de sorpresas, y lo que parece ser cierto puede tener excepciones.

En los tribunales de justicia, la prueba a menudo incluye una advertencia, como "en el balance de probabilidades" para asuntos civiles, y "más allá de toda duda razonable" para casos penales.

Pero para matemáticos como el Dr. Nick Beaton de la Universidad de Melbourne, El profesor Jan de Gier y el profesor Tony Guttmann, "más allá de toda duda razonable" simplemente no es lo suficientemente bueno. Para ellos una prueba matemática está "más allá de toda duda", y es una cosa hermosa.

Considere el teorema de Pitágoras.

Todos aprendemos en la escuela que el cuadrado del lado más largo de un triángulo rectángulo es la suma de los cuadrados de los otros dos lados. Puedes probar esto con una hoja de papel, una regla y una calculadora, y verás que es verdad.

Podrías hacer esto para mil triángulos y verás que es cierto para cada uno de esos mil triángulos.

Pero, ¿funciona el teorema de Pitágoras para todos los posibles triángulos rectángulos?

No se pueden medir todos los triángulos rectángulos que existen, de modo que el método de la regla y la calculadora no puede demostrar definitivamente que Pitágoras tiene razón.

"Haces muchas simulaciones y observas una determinada cosa numéricamente, y si observa eso una y otra vez, pensaría que probablemente siempre sea así, o es verdad "dice el Dr. Nick Beaton.

"Pero eso no es lo mismo que tener una prueba matemática en la que de hecho se puede mostrar lógicamente que algo siempre ocurre con ciertos valores de los parámetros".

Sin una prueba matemática formal, A algo como el Teorema de Pitágoras lo llamamos conjetura.

El profesor De Gier dice que una conjetura en matemáticas es un resultado que todos creen que es cierto.

"Pero no se ha demostrado lógicamente en un sentido riguroso, " él dice.

"Entonces, puede haber mucha evidencia numérica y puede haber argumentos sólidos y convincentes, pero no están estableciendo una verdad fuera de toda duda.

"Un gran ejemplo es la hipótesis de Riemann sobre los ceros de la función zeta, que se ha verificado durante los primeros 10, 000, 000, 000, 000 (diez billones) de casos. Una prueba de que es cierto para todos los casos aún falta y vale un millón de dólares, "dice el profesor De Gier.

"Demostrarlo arrojaría luz sobre muchos de los misterios que rodean la distribución de los números primos".

"Y, en ocasiones, algo parece muy convincente, pero luego se muestra, una vez que profundiza en los detalles, que en realidad no es válido y puede haber excepciones ".

Wikipedia incluso tiene una categoría para "Conjeturas refutadas":algunas, como la conjetura de Euler, se mantuvo durante cientos de años antes de ser refutado.

En el caso del teorema de Pitágoras, sin embargo, la prueba ha estado con nosotros durante miles de años. De hecho, Pitágoras no inventó la fórmula, se supo mucho antes de su tiempo. Se le ocurrió la primera prueba conocida.

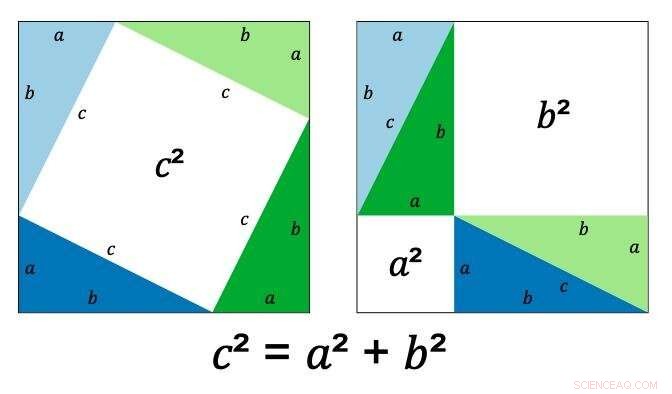
La demostración de Pitágoras utiliza el hecho indiscutible de que cualquier triángulo rectángulo puede representarse mediante dos cuadrados, uno dentro del otro, con las esquinas del cuadrado interior tocando el borde del exterior.

El cuadrado interior tiene lados de longitud c (la longitud real no importa porque c puede ser cualquier número positivo), el cuadrado exterior tiene una longitud a + b, y el triángulo que forma tiene lados a, byc (como se muestra).

Cambiar el ángulo del cuadrado interior cambia las longitudes de los tres valores.

Pitágoras mostró que al reorganizar los triángulos dentro del cuadrado, el área blanca, representado por c² en el diagrama anterior, se convierte en dos cuadrados, uno con área a² y otro con área b². Por eso, c² es siempre, no importa qué dimensiones uses, igual a a² + b².

Desde Pitágoras, Los matemáticos a lo largo de los siglos han seguido encontrando pruebas del teorema. En 1940, El matemático estadounidense Elisha Scott Loomis publicó una colección de pruebas del teorema de Pitágoras.

El equipo de la Universidad de Melbourne no es ajeno a las pruebas.

La Sociedad Australiana de Matemáticas otorgó el Premio Gavin Brown 2018 al mejor artículo al Dr. Beaton, Profesor de Gier y profesor Guttman, junto con Mireille Bousquet-Mélou de la Université de Bordeaux en Francia y Hugo Duminil-Copin de la Université de Genève en Suiza, para una prueba matemática de 2015 de la existencia y tensión superficial crítica para la adsorción de polímeros (moléculas de cadena larga) en solución.

El equipo utilizó una representación matemática de un polímero, llamada "caminata para evitar uno mismo, "que son objetos utilizados en una rama de la física matemática llamada mecánica estadística.

"Una caminata para evitar uno mismo es caminar sobre una celosía, a menudo una celosía cuadrada o una celosía de panal de abejas, donde no puede volver sobre ninguno de los pasos que ha dado. "Dice el profesor Guttmann.

"Puedes pensar en un paseo como un solo polímero, con propiedades aleatorias ".

Dr. Beaton dice que, a menudo, encontrar una prueba matemática para una conjetura es un proceso largo, proceso difícil, que implica prueba y error, trabajo gruñido y el momento eureka ocasional.

Para Pitágoras, el momento eureka fue la representación del triángulo en cuadrado en cuadrado; para el equipo de Melbourne y sus colegas, estaba encontrando la mejor manera de lidiar matemáticamente con la aleatoriedad.

"La gente intentó algunas cosas cuando se conjeturó por primera vez, pero nadie logró mucho progreso, por lo que estaba claro que se necesitaba una nueva idea, pero cuál debería ser esa nueva idea no era obvio, "dice el profesor De Gier.

Después de seguir algunos callejones sin salida, el equipo se centró en una nueva idea en matemáticas asociada con modelos de celosía, llamado "holomorficidad discreta, "que fue popularizado por el investigador ruso, el profesor Stanislav Smirnov, quien ganó la Medalla Fields por descubrimientos sobresalientes en matemáticas en 2010.

Usando este nuevo tipo de matemáticas, el equipo de Melbourne descubrió que la celosía alveolar era el lugar adecuado para demostrar su problema con los polímeros.

"Por alguna razón, las matemáticas de las caminatas para evitar uno mismo en una celosía de panal funcionaron muy bien, "Dice el profesor de Gier.

"Si quieres hacer esto en una celosía cuadrada, no funciona pero por otros problemas, la celosía cuadrada sería mejor ".

El profesor de Gier dice que una demostración matemática no es solo un ejercicio intelectual, puede decirnos cosas fundamentales sobre la naturaleza.

"Es interesante saber que sucede algo o dónde sucede, pero tener ese razonamiento lógico es más interesante porque da una idea de por qué las cosas suceden como suceden ".