
Si pensabas que las tablas de multiplicar en la escuela eran difíciles, imagina multiplicar números con miles de millones de dígitos. Crédito:Shutterstock / Nina Buday
La multiplicación de dos números es fácil, ¿Derecha?
En la escuela primaria aprendemos a hacer multiplicaciones largas como esta:
Métodos similares a este se remontan a miles de años, al menos para los antiguos sumerios y egipcios.
Pero, ¿es esta realmente la mejor manera de multiplicar dos números grandes?
En multiplicación larga, tenemos que multiplicar cada dígito del primer número por cada dígito del segundo número. Si los dos números tienen cada uno norte dígitos esa es norte 2 (o norte X norte ) multiplicaciones en total. En el ejemplo anterior, norte es 3, y tuvimos que hacer 3 2 =9 multiplicaciones.
Alrededor de 1956, El famoso matemático soviético Andrey Kolmogorov conjeturó que esta es la la mejor manera posible para multiplicar dos números juntos.
En otras palabras, no importa cómo organice sus cálculos, la cantidad de trabajo que tienes que hacer será proporcional a al menos norte 2 . El doble de dígitos significa cuatro veces más trabajo.
Kolmogorov consideró que si era posible un atajo, seguramente ya habría sido descubierto. Después de todo, la gente ha estado multiplicando números durante miles de años.
Este es un magnífico ejemplo de la falacia lógica conocida como "el argumento de la ignorancia".
Una forma mas rapida
Solo unos años después, Se demostró que la conjetura de Kolmogorov era espectacularmente errónea.
En 1960, Anatoly Karatsuba, un estudiante de matemáticas de 23 años en Rusia, descubrió un engañoso truco algebraico que reduce el número de multiplicaciones necesarias.
Por ejemplo, para multiplicar números de cuatro dígitos, en lugar de necesitar 4 2 =16 multiplicaciones, El método de Karatsuba se sale con la suya con solo nueve. Al usar su método, el doble de dígitos significa solo Tres veces más trabajo.
Esto se suma a una ventaja impresionante a medida que los números aumentan. Para números con mil dígitos, El método de Karatsuba necesita aproximadamente 17 veces menos multiplicaciones que la multiplicación larga.
Pero, ¿por qué diablos querría alguien multiplicar números tan grandes?
De hecho, hay una gran cantidad de aplicaciones. Uno de los más visibles y económicamente significativos es el de la criptografía.
Grandes números en la vida real
Cada vez que participa en una comunicación cifrada en Internet, por ejemplo, acceder a su sitio web bancario o realizar una búsqueda en la web:su dispositivo realiza una cantidad asombrosa de multiplicaciones, que involucran números con cientos o incluso miles de dígitos.
Es muy probable que su dispositivo use el truco de Karatsuba para esta aritmética. Todo esto es parte del increíble ecosistema de software que mantiene nuestras páginas web cargándose de la manera más rápida posible.
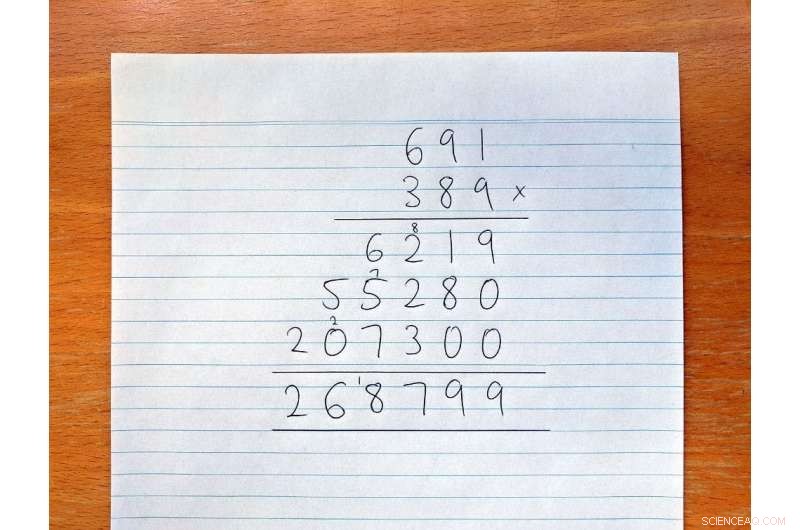
El largo camino hacia la multiplicación. Crédito:David Harvey
Para algunas aplicaciones más esotéricas, los matemáticos tienen que lidiar con números aún mayores, con millones, miles de millones o incluso billones de dígitos. Para un número tan enorme, incluso el algoritmo de Karatsuba es demasiado lento.
Un verdadero avance se produjo en 1971 con el trabajo de los matemáticos alemanes Arnold Schönhage y Volker Strassen. Explicaron cómo usar la transformada rápida de Fourier (FFT) publicada recientemente para multiplicar grandes números de manera eficiente. Los matemáticos de hoy utilizan su método de forma rutinaria para manejar números de miles de millones de dígitos.
La FFT es uno de los algoritmos más importantes del siglo XX. Una aplicación familiar en la vida diaria es el audio digital:siempre que escuche MP3, servicios de transmisión de música o radio digital, Los FFT manejan la decodificación de audio detrás de escena.
¿Una forma aún más rápida?
En su artículo de 1971, Schönhage y Strassen también hicieron una conjetura sorprendente. Para explicar, Tendré que ponerme un poco técnico por un momento.
La primera mitad de su conjetura es que debería ser posible multiplicar norte -números de dígitos que utilizan un número de operaciones básicas que es proporcional a lo más norte Iniciar sesión ( norte ) (esa es norte multiplicado por el logaritmo natural de norte ).
Su propio algoritmo no alcanzó este objetivo; eran demasiado lentos por un factor de log (log norte ) (el logaritmo del logaritmo de norte ). Sin embargo, su intuición los llevó a sospechar que les faltaba algo, y eso norte Iniciar sesión ( norte ) debería ser factible.
En las décadas desde 1971, algunos investigadores han encontrado mejoras en el algoritmo de Schönhage y Strassen. Notablemente, un algoritmo diseñado por Martin Fürer en 2007 se acercó angustiosamente al escurridizo norte Iniciar sesión ( norte ).
La segunda (y mucho más difícil) parte de su conjetura es que norte Iniciar sesión ( norte ) debería ser el límite de velocidad fundamental, que ningún algoritmo de multiplicación posible podría hacerlo mejor que éste.
¿Suena familiar?
¿Hemos llegado al límite?
Hace unas pocas semanas, Joris van der Hoeven y yo publicamos un artículo de investigación que describe un nuevo algoritmo de multiplicación que finalmente alcanza el norte Iniciar sesión ( norte ) Santo Grial, resolviendo así la parte "fácil" de la conjetura de Schönhage-Strassen.
El documento aún no ha sido revisado por pares, por lo que se justifica cierta precaución. Es una práctica estándar en matemáticas difundir los resultados de la investigación antes de que hayan sido revisados por pares.
En lugar de utilizar FFT unidimensionales, el elemento básico de todo el trabajo sobre este problema desde 1971, nuestro algoritmo se basa en multidimensional FFT. Estos gadgets no son nada nuevo:el formato de imagen JPEG ampliamente utilizado depende de FFT bidimensionales, y las FFT tridimensionales tienen muchas aplicaciones en física e ingeniería.
En nuestro periódico, usamos FFT con 1, 729 dimensiones. Esto es complicado de visualizar, pero matemáticamente no es más problemático que el caso bidimensional.
En realidad, números realmente grandes
El nuevo algoritmo no es realmente práctico en su forma actual, porque la prueba dada en nuestro artículo solo funciona para números ridículamente grandes. Incluso si cada dígito estuviera escrito en un átomo de hidrógeno, no habría suficiente espacio disponible en el universo observable para escribirlos.
Por otra parte, tenemos la esperanza de que, con más mejoras, el algoritmo podría resultar práctico para números con solo miles de millones o billones de dígitos. Si es así, bien puede convertirse en una herramienta indispensable en el arsenal del matemático computacional.
Si la conjetura completa de Schönhage-Strassen es correcta, luego desde un punto de vista teórico, el nuevo algoritmo es el final del camino, no es posible hacerlo mejor.
Personalmente, Me sorprendería mucho si la conjetura resultara errónea. Pero no debemos olvidar lo que le sucedió a Kolmogorov. Las matemáticas a veces pueden traer sorpresas.
Este artículo se ha vuelto a publicar de The Conversation con una licencia de Creative Commons. Lea el artículo original. 