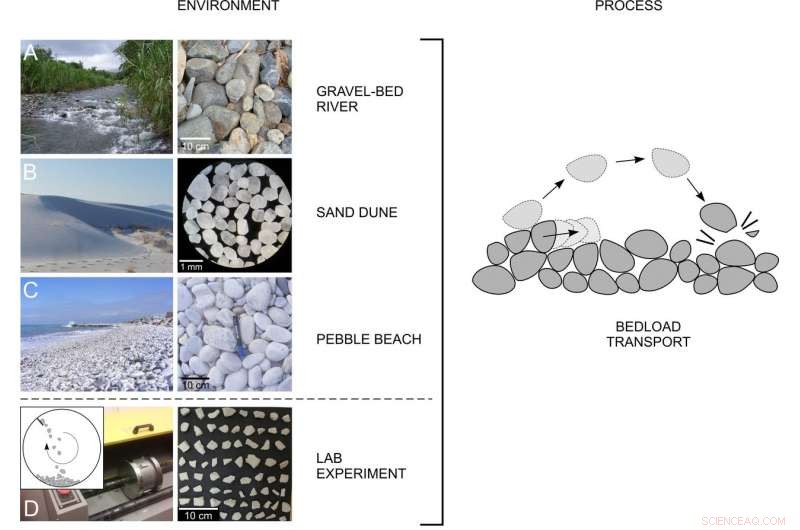
Nuevos hallazgos de un equipo dirigido por la Universidad de Pensilvania muestran que la forma de las rocas y partículas similares evoluciona de acuerdo con el mismo principio matemático. no importa si la partícula es una piedra en un río, un grano de arena en una duna o un guijarro en una playa oceánica. Crédito:Universidad de Pensilvania y Universidad de Tecnología y Economía de Budapest
El lechoso la textura suave del vidrio de playa evoca una historia de transporte turbulento, los bordes ásperos se desgastaron para producir curvas. Las mismas características suaves se pueden ver en las rocas de los ríos y las arenas de las dunas.
Combinando modelos matemáticos con experimentos de laboratorio y mediciones de campo de un río, un océano, y un campo de dunas, Un equipo dirigido por el geofísico Douglas J. Jerolmack de la Universidad de Pensilvania ha descubierto que los mismos procesos generales guían el redondeo de esos diversos tipos de partículas. Informaron sus hallazgos en la revista. Avances de la ciencia .
"Mostramos esa arena arrastrada por el viento, guijarros de río, y guijarros trabajados por las olas de la misma manera al chocar, "Jerolmack dice". Y, más importante, mostramos cómo la naturaleza selecciona las condiciones que conducen a este comportamiento universal ".
Los modelos matemáticos que explican la universalidad de esta evolución se han creado en las últimas décadas, en el esfuerzo por probar la conjetura de Poincaré, un gran avance en matemáticas puras. Resulta que las mismas ecuaciones tienen un segundo, interpretación no menos interesante como modelos para la evolución de la forma natural.
Desarrollar esta generalidad sobre cómo las partículas redondas puede ayudar a los científicos a reconstruir la historia de otras partículas, una estrategia que Jerolmack y sus colegas utilizaron para reconstruir la historia del transporte de guijarros en Marte en un artículo de Nature Communications de 2015 que afirmaba la probabilidad de agua líquida en ese planeta.
El trabajo también puede permitir a los investigadores rastrear los fragmentos de sedimento que se desprenden de partículas más grandes. Pequeño pero poderoso estos granos construyen humedales, llanuras aluviales, y playas, afectando todo, desde la resistencia a los huracanes hasta la productividad agrícola.
El equipo de investigación que incluía a Gábor Domokos, matemático de la Universidad de Tecnología y Economía de Budapest, y Tímea Novák-Szabó, un investigador postdoctoral que ha pasado tiempo en los laboratorios de Jerolmack y Domokos, previamente había reflexionado sobre cómo se redondean las rocas de los ríos. En estudios anteriores, demostraron que estas partículas primero se vuelven suaves cuando rebotan en el lecho de un río, sus esquinas afiladas astilladas, y luego se vuelven más pequeños a medida que continúan chocando con otras partículas.
En el nuevo trabajo muestran cómo la geometría simple predice una evolución de forma común para la mayoría de los sedimentos, ya sean granos de arena arrastrados por el viento, bloques de piedra caliza que chocan en un tambor giratorio en un laboratorio, o guijarros sacudidos por las olas del mar.
Usando conjuntos de datos de las dunas de White Sands de Nuevo México, un cauce puertorriqueño, una playa italiana, y el laboratorio de Domokos, los investigadores demostraron que su premisa era cierta:las colisiones con otras partículas provocaban que todas estas partículas se redondearan de manera idéntica.
Las similitudes surgen debido a las limitaciones de que las partículas que viajan a lo largo de un lecho, ya sea un río, una duna, o un océano:compartir. Estas partículas, los investigadores encontraron, tienden a originarse como formas alargadas, colisionar con partículas de tamaño similar, y hacerlo con un nivel de fuerza que favorezca el desprendimiento de pequeños fragmentos de sedimento, a diferencia de fuerzas mayores que pueden hacer que una partícula se fragmente en pedazos grandes, o fuerzas débiles que desgastarían una superficie como el papel de lija.
Con esta regla general ahora en la mano, los investigadores tienen las herramientas matemáticas que necesitan para reconstruir el historial de transporte de cualquier partícula de sedimento en función de su forma, mejorando su capacidad para predecir la evolución del paisaje a lo largo del tiempo.