La ecuación para una línea es de la forma y = mx + b, donde m representa la pendiente yb representa la intersección de la línea con el eje y. Este artículo mostrará con un ejemplo cómo podemos escribir una ecuación para la línea que tiene una pendiente dada y pasa por un punto dado.

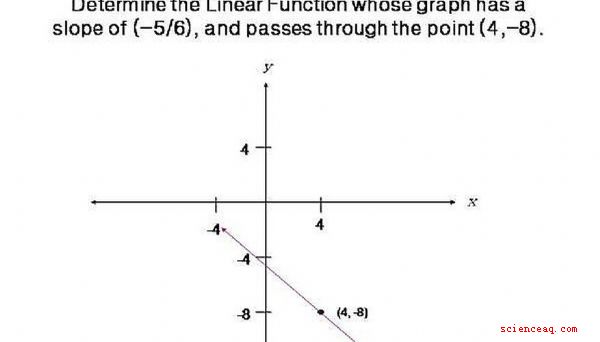
Encontraremos la función lineal cuyo gráfico tiene una pendiente de (-5 /6), y pasa por el punto (4, -8). Haga clic en la imagen para ver el gráfico.

Para encontrar la Función lineal, usaremos la forma Pendiente-Intercepción, que es y = mx + b. M es la pendiente de la línea, y b es la intersección en y. Ya tenemos la pendiente de la línea, (-5/6), por lo que reemplazaremos m con la pendiente. y = (- 5/6) x + b. Haga clic en la imagen para una mejor comprensión.

Ahora, podemos reemplazar xey con los valores del punto por el que pasa la línea, (4, -8). Cuando reemplazamos x con 4 y y con -8, obtenemos -8 = (- 5/6) (4) + b. Al simplificar la expresión, obtenemos -8 = (- 5/3) (2) + b. Cuando multiplicamos (-5/3) por 2, obtenemos (-10/3). -8 = (- 10/3) + b. Añadiremos (10/3) a ambos lados de la ecuación, y al combinar términos semejantes, obtenemos: -8+ (10/3) = b. Para sumar -8 y (10/3), necesitamos dar -8 un denominador de 3. Para hacer esto, multiplicitamos -8 por (3/3), lo que equivale a -24/3. Ahora tenemos (-24/3) + (10/3) = b, que es igual a (-14/3) = b. Haga clic en la imagen para una mejor comprensión.

Ahora que tenemos el valor para b, podemos escribir la Función lineal. Cuando reemplazamos m por (-5/6) yb por (-14/3) obtenemos: y = (- 5/6) x + (- 14/3), que es igual a y = (- 5/6 ) x- (14/3). Haga clic en la imagen para una mejor comprensión.