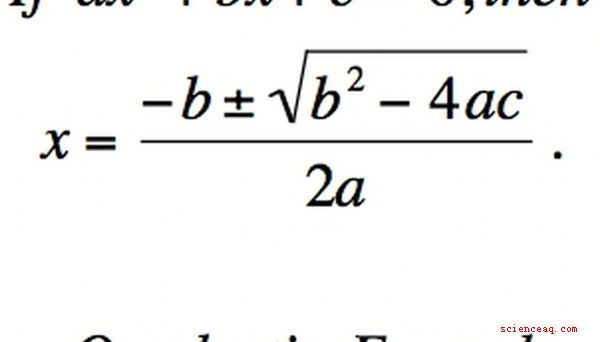
La factorización de un polinomio se refiere a encontrar polinomios de orden inferior (el máximo exponente es más bajo) que, multiplicados, producen el polinomio que se está factorizando. Por ejemplo, x ^ 2 - 1 se puede factorizar en x - 1 y x + 1. Cuando estos factores se multiplican, el -1x y el +1x se cancelan, dejando x ^ 2 y 1.
Of Limited Power
Desafortunadamente, el factoring no es una herramienta poderosa, lo que limita su uso en la vida cotidiana y en los campos técnicos. Los polinomios están fuertemente manipulados en la escuela primaria para que puedan ser factorizados. En la vida cotidiana, los polinomios no son tan amigables y requieren herramientas de análisis más sofisticadas. Un polinomio tan simple como x ^ 2 + 1 no es factorable sin usar números complejos, es decir, números que incluyen i = √ (-1). Los polinomios de orden tan bajo como 3 pueden ser prohibitivamente difíciles de factorizar. Por ejemplo, x ^ 3 - y ^ 3 factores para (x - y) (x ^ 2 + xy + y ^ 2), pero no tiene más factores sin recurrir a números complejos.
High School Science
Los polinomios de segundo orden, p. ej., x ^ 2 + 5x + 4, se tienen en cuenta regularmente en las clases de álgebra, alrededor del octavo o noveno grado. El objetivo de factorizar tales funciones es poder resolver ecuaciones de polinomios. Por ejemplo, la solución para x ^ 2 + 5x + 4 = 0 son las raíces de x ^ 2 + 5x + 4, es decir, -1 y -4. Poder encontrar las raíces de tales polinomios es básico para resolver problemas en clases de ciencias en los siguientes 2 a 3 años. Las fórmulas de segundo orden aparecen regularmente en tales clases, por ejemplo, en problemas de proyectiles y cálculos de equilibrio ácido-base.
The Quadratic Formula
Al encontrar mejores herramientas para reemplazar el factoring, debe recordar cuál es el propósito del factoring en primer lugar: resolver ecuaciones. La fórmula cuadrática es una forma de evitar la dificultad de factorizar algunos polinomios mientras se sigue resolviendo una ecuación. Para las ecuaciones de polinomios de segundo orden (es decir, de la forma ax ^ 2 + bx + c), la fórmula cuadrática se usa para encontrar las raíces del polinomio y, por lo tanto, la solución de la ecuación. La fórmula cuadrática es x = [-b +/- √ (b ^ 2 - 4ac)] /[2a], donde +/- significa "más o menos". Observe que no es necesario escribir (x - root1) (x - root2) = 0. En lugar de descomponer en factores para resolver la ecuación, la solución de la fórmula se puede resolver directamente sin factorizar como un paso intermedio, aunque el método se basa en factorización.
Esto no quiere decir que el factoring sea prescindible. Si los estudiantes aprendieran la ecuación cuadrática de resolver ecuaciones de polinomios sin aprender a factorizar, se reduciría la comprensión de la ecuación cuadrática.
Ejemplos
Esto no quiere decir que la factorización de polinomios nunca se haga afuera de clases de álgebra, física y química. Las calculadoras financieras de mano realizan un cálculo de interés diario usando una fórmula que es la factorización de los pagos futuros con el componente de interés retirado (ver diagrama). En ecuaciones diferenciales (ecuaciones de tasas de cambio), la factorización de polinomios de derivados (tasas de cambio) se realiza para resolver lo que se denominan "ecuaciones homogéneas de orden arbitrario". Otro ejemplo es el cálculo introductorio, en el método de fracciones parciales para facilitar la integración (resolver para el área bajo una curva).
Soluciones computacionales y el uso del aprendizaje en segundo plano
Estos ejemplos son , por supuesto, lejos de todos los días. Y cuando el factoring se pone difícil, tenemos calculadoras y computadoras para hacer el trabajo pesado. En lugar de esperar una coincidencia uno a uno entre cada tema matemático que se enseña y los cálculos diarios, consulte la preparación que el tema proporciona para un estudio más práctico. El factoring debe ser apreciado por lo que es: un paso hacia los métodos de aprendizaje para resolver ecuaciones cada vez más realistas.