Este artículo mostrará cómo esbozar los gráficos de la función de raíz cuadrada al usar solo tres valores diferentes para 'x', luego encontrar los puntos a través de los cuales se dibuja la gráfica de las ecuaciones /funciones, también mostrará cómo los gráficos Verticalmente se traduce (se mueve hacia arriba o hacia abajo), se traduce horizontalmente (se mueve hacia la izquierda o hacia la derecha) y cómo el gráfico hace simultáneamente ambas traducciones.
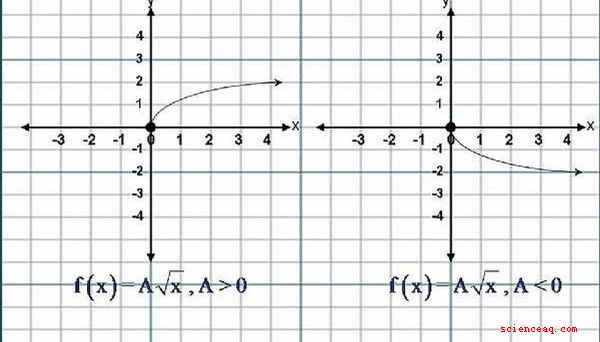
La ecuación de una función de raíz cuadrada tiene la forma, .. . y = f (x) = A√x, donde (A) no debe ser igual a cero (0). Si (A) es mayor que Cero (0), es decir (A) es un Número Positivo, entonces el La forma del gráfico de la función de raíz cuadrada es similar a la mitad superior de la letra, 'C'. Si (A) es menor que cero (0), es decir (A) es un número negativo, la forma del gráfico es similar a la de la mitad inferior de la letra 'C'. Haga clic en la imagen para verla mejor.
Para dibujar el gráfico de la ecuación, ... y = f (x) = A√x, elegimos Tres valores para 'x', x = ( -1), x = (0) yx = (1). Sustituimos cada valor de 'x' en la Ecuación, ... y = f (x) = A√x y obtenemos el correspondiente valor correspondiente para cada 'y'.
Dado y = f (x) = A√x, donde (A) es un Número Real y (A) no es igual a Cero (0), y sustituyendo, x = (-1) en la Ecuación obtenemos y = f (-1) = A√ ( -1) = i (que es un número imaginario). Entonces, el Primer Punto no tiene coordenadas reales, por lo tanto, no se puede dibujar ningún gráfico a través de este punto. Ahora sustituyendo, x = (0), obtenemos y = f (0) = A√ (0) = A (0) = 0. Entonces, el segundo punto tiene coordenadas (0,0). Y sustituyendo x = (1) obtenemos y = f (1) = A√ (1) = A (1) = A. Entonces el tercer punto tiene coordenadas (1, A). Como el primer punto tenía coordenadas que no eran reales, ahora buscamos un cuarto punto y elegimos x = (2). Ahora sustituya x = (2) en y = f (2) = A√ (2) = A (1.41) = 1.41A. Entonces el cuarto punto tiene coordenadas (2,1.41A). Ahora esbozamos la curva a través de estos tres puntos. Haga clic en la imagen para ver mejor.
Dada la ecuación y = f (x) = A√x + B, donde B es cualquier número real, el gráfico de esta ecuación se traduciría verticalmente (B) unidades. Si (B) es un Número Positivo, el Gráfico se moverá hacia arriba (B) unidades, y si (B) es un Número Negativo, el Gráfico se moverá hacia abajo (B) unidades. Para delinear los gráficos de esta ecuación, seguimos las instrucciones y usamos los mismos valores de 'x' del paso n. ° 3. Haga clic en la imagen para obtener una mejor visión.
Dada la ecuación y = f (x) = A√ (x - B) donde A y B son números reales, y (A) no es igual a Cero (0) yx ≥ B. La gráfica de esta ecuación traduce las unidades horizontalmente (B). Si (B) es un Número Positivo, el Gráfico se moverá a las unidades Derechas (B) y si (B) es un Número Negativo, el Gráfico se moverá a las unidades Izquierdas (B). Para bosquejar los gráficos de esta ecuación, primero establecemos la expresión, 'x - B', que está debajo del signo radical Mayor o igual a cero, y resolvemos por 'x'. Es decir, ... x - B ≥ 0, luego x ≥ B.
Ahora usaremos los siguientes tres valores para 'x', x = (B), x = (B + 1) y x = (B + 2). Sustituimos cada valor de 'x' en la ecuación, ... y = f (x) = A√ (x - B) y obtenemos el correspondiente valor correspondiente para cada 'y'.
Dado y = f (x) = A√ (x - B), donde A y B son números reales, y (A) no es igual a cero (o) donde x ≥ B. Sustituyendo, x = (B) en la ecuación obtenemos y = f (B) = A√ (BB) = A√ (0) = A (0) = 0. Entonces, el primer punto tiene coordenadas (B, 0). Ahora Sustituyendo, x = (B + 1), obtenemos y = f (B + 1) = A√ (B + 1 - B) = A√1 = A (1) = A. Entonces el Segundo Punto tiene Coordenadas ( B + 1, A) y Sustituyendo x = (B + 2) obtenemos y = f (B + 2) = A√ (B + 2-B) = A√ (2) = A (1.41) = 1.41A . Entonces, el tercer punto tiene coordenadas (B + 2,1.41A). Ahora esbozamos la curva a través de estos tres puntos. Haga clic en la imagen para ver mejor.
Dado y = f (x) = A√ (x - B) + C, donde A, B, C son números reales y (A) no iguales a Cero (0) y x ≥ B. Si C es un número positivo, entonces la gráfica en el PASO n. ° 7 traducirá unidades verticalmente (C). Si (C) es un Número Positivo, el Gráfico se moverá hacia arriba (C) unidades, y si (C) es un Número Negativo, el Gráfico se moverá hacia abajo (C) unidades. Para esbozar los gráficos de esta ecuación, seguimos las instrucciones y usamos los mismos valores de 'x' del paso 7. Haga clic en la imagen para obtener una mejor visión.