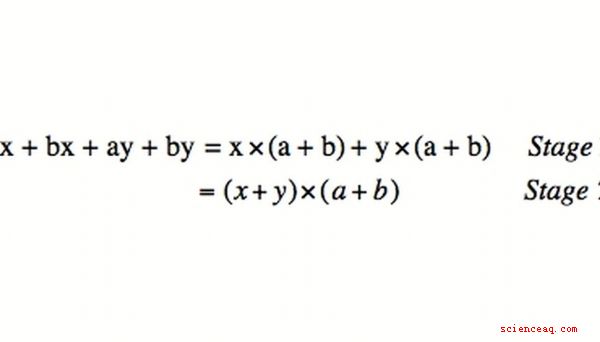
Los cuadráticos son polinomios de segundo orden, es decir, ecuaciones de variables con exponentes que suman como máximo 2. Por ejemplo, x ^ 2 + 3x + 2 es un cuadrático. Factorizarlo significa encontrar sus raíces, de modo que (x-root1) (x-root2) sea igual a la cuadrática original. Ser capaz de factorizar tal fórmula es lo mismo que ser capaz de resolver la ecuación x ^ 2 + 3x + 2 = 0, ya que las raíces son los valores de x donde el polinomio es igual a cero.
Signos para reverso Método FOIL
El método inverso FOIL para factorizar cuadráticos pregunta: ¿Cómo se completa la forma (? X +?) (? X +?) Cuando se factoriza ax ^ 2 + bx + c (a, b, c constantes)? Hay algunas reglas para el factoring que pueden ayudar a responder esto.
"FOIL" recibe su nombre de su método de multiplicar los factores. Para multiplicar, digamos, (2x + 3) y (4x + 5), 2 y 4 se llaman "primero", 3 y 5 se llaman "último", 3 y 4 se llaman "interno" y se llaman 2 y 5 "exterior." Por lo tanto, la forma podría escribirse como (FOx + LI) (FIx + LO).
Una regla de factorización útil para ax ^ 2 + bx + c es notar que si c > 0, entonces LI y LO deben ser ambos positivos o ambos negativos. Del mismo modo, si a es positivo, FO y FI deben ser tanto positivos como negativos. Si c es negativo, entonces LI o LO es negativo, pero no ambos. Nuevamente, lo mismo vale para a, FO y FI.
Si a, c > 0, pero b < 0, entonces la factorización debe hacerse de modo que LI y LO sean ambos negativos o FO y FI son ambos negativos (No importa cuál, ya que ambas maneras conducirán a una factorización.)
Reglas para factorizar cuatro términos
Una regla para factorizar cuatro términos de variables es sacar términos comunes. Por ejemplo, los pares en xy-5y + 10-2x tienen términos comunes. Sacarlos da: y (x-5) + 2 (5-x). Tenga en cuenta la similitud de lo que está entre paréntesis. Por lo tanto, también pueden extraerse: y (x-5) -2 (x-5) se convierte en (y-2) (x-5). Esto se denomina "factorizar por agrupamiento".
Ampliar agrupamiento a cuadráticos
La regla para factorizar cuatro términos se puede extender a cuadráticos. La regla para hacerlo es: encontrar factores de a --- c que sumen a b. Por ejemplo, x ^ 2-10x + 24 tiene a --- c = 24 yb = -10. 24 tiene 6 y 4 como factores, que se suman a 10. Esto nos da una pista sobre la respuesta final que estamos buscando: -6 y -4 también se multiplican para dar 24, y suman a b = -10.
Entonces ahora el cuadrático se reescribe con b split up: x ^ 2-6x-4x + 24. Ahora la fórmula se puede factorizar como al factorizar por agrupamiento, siendo el primer paso: x (x-6) + 4 (6-x).