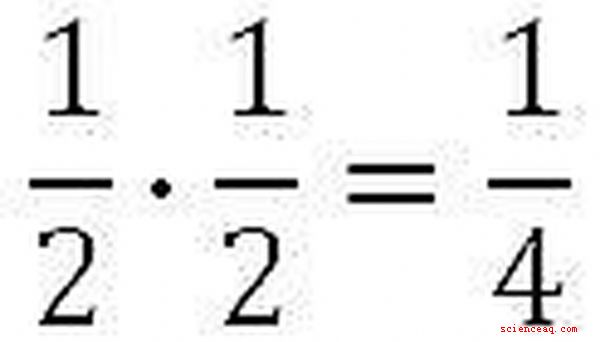
Este es el Artículo 1 de una serie de artículos independientes sobre probabilidad básica. Un tema común en la probabilidad introductoria es resolver problemas relacionados con el lanzamiento de monedas. Este artículo le muestra los pasos para resolver los tipos más comunes de preguntas básicas sobre este tema.

En primer lugar, tenga en cuenta que es probable que el problema haga referencia a una moneda "justa". Todo esto significa que no estamos tratando con una moneda de "truco", como una que ha sido ponderada para aterrizar en un cierto lado con más frecuencia de lo que debería.

En segundo lugar, problemas como este nunca involucra cualquier tipo de tontería, como la moneda que aterriza en su borde. A veces los estudiantes intentan cabildear para que una pregunta se considere nula e inválida debido a algún escenario descabellado. No incluya nada en la ecuación, como resistencia al viento, ni si la cabeza de Lincoln pesa más que su cola, o algo similar. Estamos tratando con 50/50 aquí. Los profesores realmente se molestan cuando hablan de cualquier otra cosa.

Dicho todo esto, aquí hay una pregunta muy común: "una moneda justa cae en la cabeza cinco veces seguidas. ¿Cuáles son las probabilidades de que aterrice? se dirige a la próxima tapa? " La respuesta a la pregunta es simplemente 1/2, 50% o 0.5. Eso es. Cualquier otra respuesta es incorrecta.

Deja de pensar en lo que sea que estés pensando en este momento. Cada lanzamiento de una moneda es totalmente independiente. La moneda no tiene memoria. La moneda no se "aburre" de un resultado dado, y desea cambiar a otra cosa, ni tiene ningún deseo de continuar un resultado particular ya que está "en racha". Para estar seguro, cuantas más veces arrojes una moneda, más cerca estarás de que el 50% de los lanzamientos sean cabezas, pero eso aún no tiene nada que ver con un lanzamiento individual. Estas ideas comprenden lo que se conoce como la falacia del jugador. Para más información, vea la sección de Recursos.

Aquí hay otra pregunta común: "Una moneda justa es volteada dos veces. ¿Cuáles son las posibilidades de que caiga sobre las cabezas en ambos lanzamientos?" Lo que estamos tratando aquí es dos eventos independientes, con una condición "y". Dicho de manera más simple, cada lanzamiento de la moneda no tiene nada que ver con ningún otro lanzamiento. Además, estamos tratando con una situación en la que necesitamos que ocurra una cosa "y" otra cosa ".

En situaciones como la anterior, multiplicamos las dos probabilidades independientes juntas. En este contexto, la palabra "y" se traduce en multiplicación. Cada lanzamiento tiene una probabilidad de 1/2 de aterrizar en la cabeza, por lo que multiplicamos 1/2 por 1/2 para obtener 1/4. Eso significa que cada vez que realizamos este experimento de dos vueltas, tenemos una posibilidad de 1/4 de obtener cabezas-cabezas como resultado. Tenga en cuenta que también podríamos haber hecho este problema con decimales, para obtener 0.5 veces 0.5 = 0.25.

Aquí está el modelo final de pregunta discutido en este artículo: "Una moneda justa se da vuelta 20 veces seguidas. ¿Cuáles son las posibilidades de que caiga en las cabezas todo el tiempo? Exprese su respuesta utilizando un exponente ". Como vimos antes, estamos tratando con una condición "y" para eventos independientes. Necesitamos que el primer flip sea head, y el segundo flip sea heads, y el tercero, etc.

Debemos calcular 1/2 veces 1/2 por 1/2, repetimos un total de 20 veces. La forma más simple de representar esto se muestra a la izquierda. Está (1/2) elevado a la vigésima potencia. El exponente se aplica tanto al numerador como al denominador. Dado que 1 a la potencia de 20 es solo 1, también podríamos escribir nuestra respuesta como 1 dividido por (2 a la 20 potencia).

Es interesante notar que las probabilidades reales de que ocurra lo anterior son aproximadamente uno en un millón. Si bien es poco probable que una persona en particular experimente esto, si le pidieras a cada estadounidense que realizara este experimento de manera honesta y precisa, un buen número de personas reportaría el éxito.

Los estudiantes deberían asegurarse de que se sienten cómodos trabajando con los conceptos básicos de probabilidad discutidos en este artículo, ya que aparecen con bastante frecuencia.