El entrelazamiento es una propiedad de la física cuántica que se manifiesta cuando dos o más sistemas interactúan de tal manera que sus estados cuánticos no pueden describirse de forma independiente. En la terminología de la física cuántica se dice que están entrelazados, es decir, fuertemente correlacionados. El entrelazamiento es de suma importancia para la computación cuántica. Cuanto mayor sea el entrelazamiento, más optimizada y eficiente será la computadora cuántica.
Un estudio realizado por investigadores del Departamento de Física del Instituto de Geociencias y Ciencias Exactas (IGCE-Unesp) de la Universidad Estadual Paulista, en Río Claro, Brasil, probó un nuevo método para cuantificar el entrelazamiento y las condiciones para su maximización. Las aplicaciones incluyen la optimización de la construcción de una computadora cuántica.
Un artículo sobre el estudio se publica como carta en Physical Review B. .
El estudio mostró cómo el teorema de Hellmann-Feynman se desmorona en condiciones específicas. El teorema describe la dependencia de la propia energía del sistema de un parámetro de control y es una parte clave de la mecánica cuántica utilizada en disciplinas que van desde la química cuántica hasta la física de partículas.
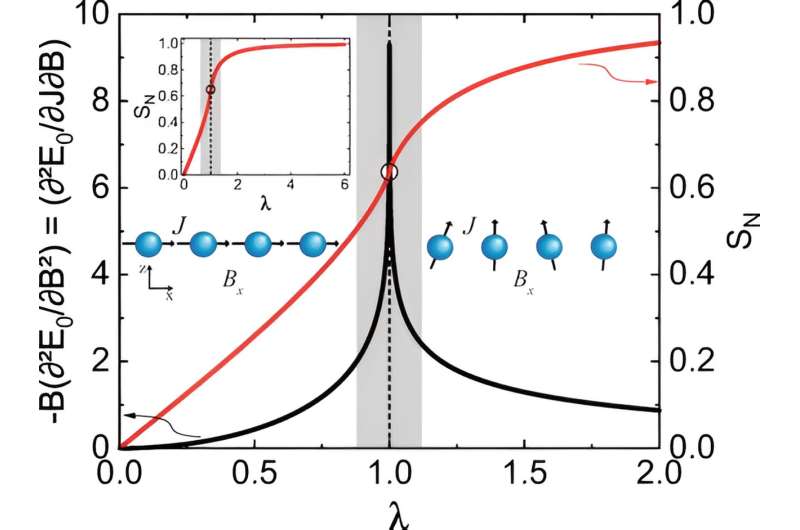
"En pocas palabras, proponemos un análogo cuántico del parámetro Grüneisen ampliamente utilizado en termodinámica para explorar la temperatura finita y los puntos críticos cuánticos. En nuestra propuesta, el parámetro cuántico Grüneisen cuantifica el entrelazamiento, o entropía de von Neumann, en relación con un parámetro de control, que puede ser un campo magnético o un cierto nivel de presión, por ejemplo", dijo a Agência FAPESP Valdeci Mariano de Souza, último autor del artículo y docente del IGCE-Unesp.
"Utilizando nuestra propuesta, demostramos que el entrelazamiento se maximizará cerca de los puntos críticos cuánticos y que el teorema de Hellmann-Feynman se desmorona en un punto crítico".
Para Souza, los resultados contribuyen a la investigación en física básica y también podrían impactar directamente en la computación cuántica. Recordando la predicción de 1965 del cofundador de Intel, Gordon Moore, de que el número de transistores utilizados en las computadoras convencionales se duplicaría cada dos años, dijo que este rápido crecimiento en el poder de las computadoras clásicas no podía durar, mientras que los recientes avances tecnológicos están permitiendo que la computación cuántica progrese a pasos agigantados y límites, con gigantes como Google e IBM a la cabeza.
"En la informática convencional, el lenguaje binario en términos de ceros y unos se utiliza para procesar información. La mecánica cuántica, sin embargo, superpone estados y aumenta enormemente la capacidad de procesamiento. De ahí el creciente interés en la investigación sobre el entrelazamiento cuántico", explicó.
El estudio fue propuesto y diseñado por Souza, e importantes aportes fueron realizados por Lucas Squillante, investigador postdoctoral que él supervisa. Los otros colaboradores fueron Antonio Seridonio (UNESP Ilha Solteira), Roberto Lagos-Mónaco (UNESP Rio Claro), Luciano Ricco (Universidad de Islandia) y Aniekan Magnus Ukpong (Universidad de KwaZulu-Natal, Sudáfrica).
Más información: Lucas Squillante et al, Parámetro de Grüneisen como brújula de entrelazamiento y descomposición del teorema de Hellmann-Feynman, Physical Review B (2023). DOI:10.1103/PhysRevB.108.L140403
Información de la revista: Revisión física B
Proporcionado por la FAPESP