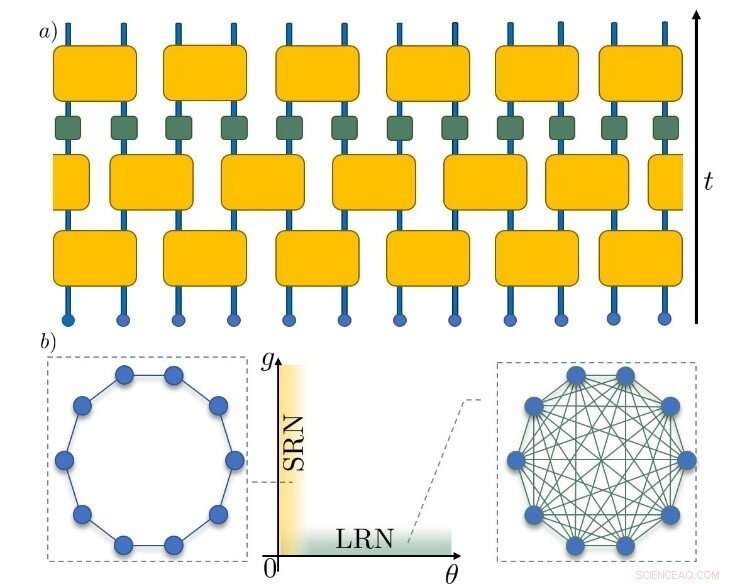
Figura 1. Representación esquemática del modelo de Mapa de Circuito Unitario. (a) La flecha negra a la derecha muestra la dirección del tiempo a medida que evolucionan las partículas, representadas por pequeños círculos azules. Los cuadrados amarillos representan las transformaciones que acoplan las partículas. Los cuadrados verdes indican las transformaciones no lineales que inducen el caos. (b) Dependiendo de los parámetros seleccionados, el acoplamiento entre partículas puede ser de corto alcance (izquierda) o de largo alcance (derecha). En última instancia, esto afecta las escalas de tiempo emergentes de la dinámica caótica. Crédito:Instituto de Ciencias Básicas
Un ejemplo popular de comportamiento caótico es el efecto mariposa:una mariposa puede batir sus alas en algún lugar del Océano Atlántico y causar un tornado en Colorado. Esta notable fábula ilustra cómo la extrema sensibilidad de la dinámica de los sistemas caóticos puede producir resultados dramáticamente diferentes a pesar de las ligeras diferencias en las condiciones iniciales. Las leyes fundamentales de la naturaleza que rigen la dinámica de los sistemas físicos son inherentemente no lineales, lo que a menudo conduce al caos y la subsiguiente termalización.
Sin embargo, uno puede preguntarse por qué no hay un aumento desenfrenado de los tornados en Colorado causados por una enorme decepción de las mariposas en los asuntos globales, como por ejemplo el calentamiento global. Esto se debe a que la dinámica física, aunque caótica, es capaz de demostrar estados notablemente estables. Un ejemplo es la estabilidad de nuestro sistema solar:obedece leyes no lineales de la física, que aparentemente pueden inducir el caos en el sistema.
La razón de esta estabilidad se basa en el hecho de que los sistemas débilmente caóticos pueden mostrar dinámicas periódicas muy ordenadas que pueden durar millones de años. Este descubrimiento fue realizado en la década de 1950 por los grandes matemáticos Kolmogorov, Arnold y Moser. Su descubrimiento, sin embargo, funciona solo en el caso de sistemas con una pequeña cantidad de elementos que interactúan. Si el sistema incluye muchas partes constituyentes, entonces su destino no se entiende tan bien.
Investigadores del Centro de Física Teórica de Sistemas Complejos (PCS) dentro del Instituto de Ciencias Básicas (IBS), Corea del Sur, recientemente introdujeron un marco novedoso para caracterizar dinámicas débilmente caóticas en sistemas complejos que contienen una gran cantidad de partículas constituyentes. Para lograrlo, utilizaron un modelo basado en computación cuántica, el mapa de circuitos unitarios, para simular el caos.
Investigar escalas de tiempo de caoticidad es una tarea desafiante que requiere métodos computacionales eficientes. El modelo de mapa de circuito unitario implementado en este estudio aborda este requisito. "El modelo permite una propagación eficiente y sin errores de los estados en el tiempo", explica Merab Malishava, "lo cual es esencial para modelar una caoticidad extremadamente débil en sistemas grandes. Dichos modelos se usaron antes para lograr tiempos de evolución no lineal sin precedentes, que era también hecho en nuestro grupo."
Como resultado, pudieron clasificar la dinámica dentro del sistema mediante la identificación de escalas de tiempo y longitud que emergen a medida que la termalización se ralentiza drásticamente. Los investigadores descubrieron que si las partes constituyentes están conectadas en forma de red de largo alcance (LRN, por sus siglas en inglés) (por ejemplo, de manera general), la dinámica de termalización se caracteriza por una escala de tiempo única, llamada tiempo de Lyapunov. Sin embargo, si el acoplamiento es de naturaleza de red de corto alcance (SRN, por sus siglas en inglés) (por ejemplo, el vecino más cercano), surge una escala de longitud adicional relacionada con la congelación de partes más grandes del sistema durante períodos prolongados con raras salpicaduras caóticas.
Por lo general, los estudios sobre dinámicas tan sensibles se realizan utilizando técnicas de análisis del comportamiento de los observables. Estas técnicas se remontan a la década de 1950 cuando se realizaron los primeros experimentos sobre caoticidad y termalización. Los autores identificaron un nuevo método de análisis mediante la investigación de la escala del espectro de Lyapunov.
Merab Malishava dice:"Los métodos anteriores pueden tener resultados ambiguos. Eliges un observable y aparentemente notas la termalización y piensas que la dinámica es caótica. Sin embargo, si se estudia otro observable, desde otra perspectiva, concluyes que el sistema está congelado y nada". cambia, lo que significa que no hay termalización. Esta es la ambigüedad, que superamos. El espectro de Lyapunov es un conjunto de escalas de tiempo que caracterizan la dinámica total y completamente. Y lo que es más, ¡es el mismo desde todos los puntos de vista! Único e inequívoco". /P>
Los resultados no sólo son interesantes desde un punto de vista fundamental. También tienen el potencial de arrojar luz sobre las realizaciones de las computadoras cuánticas. La computación cuántica requiere una dinámica coherente, lo que significa que no hay termalización. En el trabajo actual, se estudió una desaceleración dramática de la dinámica térmica con cantidades emergentes casi conservadas. La cuantificación de este caso posiblemente podría explicar fenómenos como la localización de muchos cuerpos, que es una de las ideas básicas para evitar la termalización en las computadoras cuánticas.
Otro gran logro del estudio se relaciona con la aplicabilidad de los resultados a una gran mayoría de modelos físicos que van desde redes de osciladores simples hasta dinámicas de redes de espín complejas. El Dr. Sergej Flach, líder del grupo de investigación y director de PCS explica:"Hemos estado trabajando durante cinco años en el desarrollo de un marco para clasificar la dinámica débilmente caótica en sistemas macroscópicos, lo que resultó en una serie de trabajos que avanzaron significativamente en el área. "Dejamos de lado los estudios caso por caso estrictamente enfocados a favor de fomentar un enfoque conceptual que sea confiable y relacionable en un gran número de realizaciones físicas. Este trabajo específico es un componente muy importante en el marco antes mencionado. Descubrimos que un traditional way of looking at things is sometimes not the most informative and offered a novel alternative approach. Our work by no means stops here, as we look forward to advancing science with more breakthrough ideas."
This research was recently published in Physical Review Letters. Freezing upon heating:Formation of dynamical glass