Para que dos formas sean congruentes, cada una debe tener el mismo número de lados y sus ángulos también deben ser iguales. Las formas más fáciles de determinar si dos formas son congruentes es rotar una de las formas hasta que esté alineada con la otra, o simplemente juntar las formas una encima de la otra para ver si sobresale algún extremo. Si no puede mover las formas físicamente, puede usar fórmulas para determinar si las formas son congruentes.

Círculos congruentes

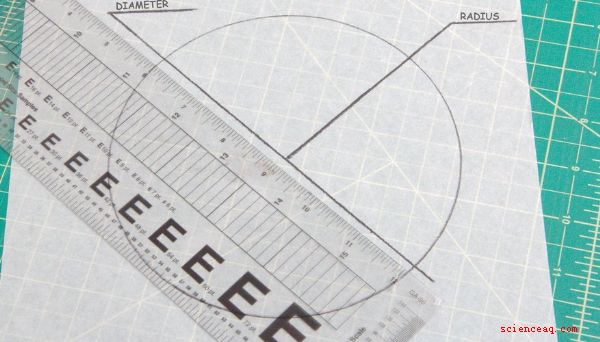
Todos los círculos tienen el mismo ángulo de 360 ​​grados. El único factor para determinar la congruencia de dos círculos es comparar su tamaño. El diámetro es una línea recta que atraviesa el centro del círculo desde el borde hasta el borde, mientras que el radio de un círculo es la longitud desde su centro hasta su borde exterior. La medición de cualquiera de estos en ambos círculos demostrará si son congruentes.

Paralelogramos

Un paralelogramo tiene dos pares de lados paralelos, como cuadrados y rectángulos. Los lados o ángulos opuestos de un paralelogramo tienen la misma medida, por lo que es necesario tomar dos medidas angulares o laterales en un paralelogramo, una de cada par de lados, para comparar la congruencia con otra forma.

Triángulos

Para encontrar la congruencia de los triángulos, debe determinar el tamaño de cada ángulo o lado, ya que los tres pueden ser diferentes. Hay tres postulados que se pueden usar para identificar triángulos congruentes. El postulado de SSS es cuando mides los tres lados de cada triángulo. El postulado de ASA dice que si dos ángulos y su lado de conexión coinciden con el del otro triángulo, entonces son congruentes. El postulado SAS hace lo contrario, mide dos lados y su ángulo de conexión para comparar con el otro triángulo.

Teoremas para triángulos congruentes

Dos teoremas son útiles para encontrar triángulos congruentes. El teorema de AAS dice que si dos ángulos y un lado que no conecta los dos son iguales a los de otro triángulo, entonces son congruentes. El teorema de hipotenusa y pierna solo se aplica a triángulos con un ángulo de 90 grados o "derecho". Esto es cuando mides la hipotenusa, el lado opuesto al ángulo de 90 grados, y uno de los otros lados del triángulo, para comparar con la otra forma.