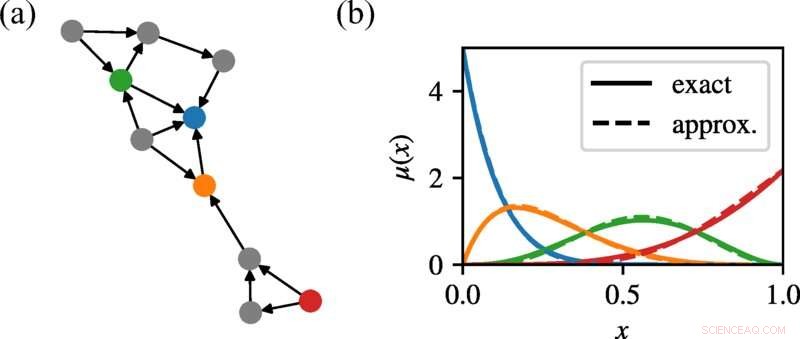
En (a) mostramos una red que crece aleatoriamente con un grado de Poisson. En (b) mostramos los márgenes posteriores de cuatro nodos representativos, coloreados para que coincidan con (a), comparando los obtenidos por nuestro método con los resultados exactos de la enumeración exhaustiva. A pesar de la presencia de ciclos cortos, nuestro enfoque de propagación de creencias se aproxima bastante a los marginales, igualando no solo las medias sino también las formas de estas distribuciones. Crédito:Revisión física E (2022). DOI:10.1103/PhysRevE.105.L052303
El mundo está plagado de rankings y ordenamientos. Aparecen en el tenis, como en el Abierto de Francia, que termina con una clasificación final de jugadores campeones. Aparecen en pandemias, como cuando los funcionarios de salud pública pueden registrar nuevas infecciones y usar el rastreo de contactos para esbozar redes de propagación de COVID-19. Los sistemas de competencia, conflicto y contagio pueden dar lugar a jerarquías.
Sin embargo, estas jerarquías se observan a posteriori. Eso dificulta conocer las verdaderas clasificaciones del sistema:¿Quién fue en realidad el mejor jugador? ¿Quién infectó a quién? "No se puede retroceder en el tiempo y saber exactamente cómo sucedió esto", dice el becario postdoctoral de SFI, George Cantwell. Se podría construir un modelo de la red y comparar todos los resultados posibles, pero tal enfoque de fuerza bruta rápidamente se vuelve insostenible. Si estuviera tratando de clasificar un grupo con solo 60 participantes, por ejemplo, la cantidad de permutaciones posibles alcanza la cantidad de partículas en el universo conocido.
Para un artículo reciente publicado en Physical Review E , Cantwell colaboró con el profesor de SFI Cris Moore, científico informático y matemático, para describir una nueva forma de evaluar las clasificaciones. Su objetivo no era encontrar una verdadera jerarquía, sino calcular la dispersión de todas las jerarquías posibles, con cada una ponderada por su probabilidad.
"Estábamos dispuestos a no estar exactamente en lo cierto, pero queríamos obtener buenas respuestas con cierto sentido de lo buenas que son", dice Cantwell. El nuevo algoritmo está inspirado en la física:los rangos se modelan como entidades que interactúan y que pueden moverse hacia arriba o hacia abajo. A través de esa lente, el sistema se comporta como un sistema físico que puede analizarse utilizando métodos de la teoría del vidrio giratorio.
Poco después del comienzo de la pandemia de COVID-19, Cantwell y Moore comenzaron a pensar en modelos de cómo se propaga la enfermedad a través de una red. Rápidamente reconocieron la situación como un problema de orden que surge con el tiempo, similar a la difusión de un meme en las redes sociales o la aparición de clasificaciones de campeonatos en los deportes profesionales. "¿Cómo ordenas las cosas cuando tienes información incompleta?" pregunta Cantwell.
Comenzaron imaginando una función que pudiera obtener un ranking de precisión. Por ejemplo:una buena clasificación sería aquella que concuerde con los resultados de los enfrentamientos el 98 % de las veces. Una clasificación que concuerda con los resultados solo el 10% de las veces sería pésima, peor que lanzar una moneda al aire sin ningún conocimiento previo.
Un problema con las clasificaciones es que normalmente son discretas, lo que significa que siguen los números enteros:1, 2, 3, etc. Ese orden sugiere que la "distancia" entre el primer y el segundo miembro es la misma que entre el segundo y el tercero. Pero ese no es el caso, dice Cantwell. Los mejores jugadores en un juego, en todo el mundo, estarán muy cerca en términos de habilidad, por lo que la diferencia entre los mejores jugadores puede ser más cercana de lo que parece.
"Muy a menudo ves que los jugadores de menor rango pueden vencer a los jugadores de mayor rango, y la única forma en que el modelo puede tener sentido y ajustarse a los datos es juntando todos los rangos", dice Cantwell.
Cantwell y Moore describieron un sistema que evalúa las clasificaciones basándose en un sistema de numeración continua. Una clasificación podría asignar cualquier número real (número entero, fracción, decimal repetido infinitamente) a un jugador en la red. "Es más fácil trabajar con números continuos", dice Cantwell, y esos números continuos todavía se pueden traducir a clasificaciones discretas.
Además, este nuevo enfoque se puede utilizar para predecir algo sobre el futuro, como el resultado de un torneo de tenis, y también para inferir algo sobre el pasado, como la propagación de una enfermedad. "Estas clasificaciones podrían decirnos el orden de los equipos deportivos de mejor a peor. Pero también podrían decirnos el orden en que las personas de una comunidad se infectaron con una enfermedad", dice Moore. "Incluso antes de su postdoctorado, George estaba trabajando en este problema como una forma de mejorar el rastreo de contactos en una epidemia. Así como podemos predecir qué equipo ganará un juego, podemos inferir cuál de las dos personas infectó a la otra cuando entraron en contacto". unos con otros".
En el trabajo futuro, los investigadores dicen que planean investigar algunas de las preguntas más profundas que han surgido. Más de una clasificación puede estar de acuerdo con los datos pero estar radicalmente en desacuerdo con otras clasificaciones, por ejemplo. O una clasificación que parece incorrecta puede tener una gran incertidumbre pero no ser inexacta. Cantwell dice que también quiere comparar las predicciones del modelo con los resultados de las competiciones del mundo real. En última instancia, dice, el modelo podría usarse para mejorar las predicciones en una amplia gama de sistemas que conducen a clasificaciones, desde modelos de enfermedades infecciosas hasta apuestas deportivas.
Cantwell dice que conservará su dinero, por ahora. "No estoy del todo listo para empezar a apostar por ello", dice. ¿Puede el algoritmo de "propagación de creencias" describir con precisión sistemas complejos en red?