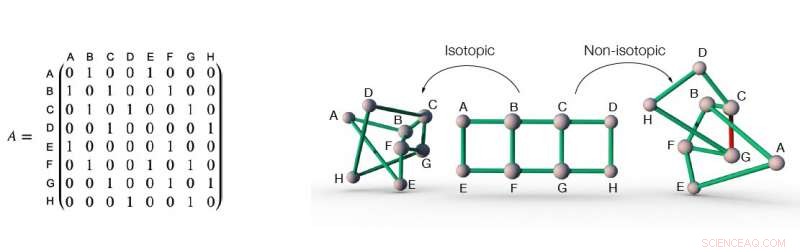
La matriz de adyacencia de una red (izquierda), y tres incrustaciones diferentes de esta red en el espacio (derecha). La matriz de adyacencia de una red registra información de la conectividad de la red. Por ejemplo, en la red de la figura, los nodos A y B están conectados por un enlace, por lo tanto, el elemento de la matriz de adyacencia en la intersección de la fila A y la columna B es uno. Similar, los nodos A y C no están conectados por un enlace, por lo tanto, el elemento de la matriz de adyacencia en la intersección de la fila A y la columna C es cero. Las dos primeras incorporaciones de red de la red descritas por la matriz de adyacencia de la izquierda son isotópicas entre sí, porque pueden transformarse entre sí simplemente "aplanar" la incrustación, sin necesidad de abrir ningún enlace. Por otra parte, la incrustación de la derecha no es isotópica a las otras dos incrustaciones, porque para transformarlo en los otros dos, al menos un enlace (el enlace rojo, por ejemplo) debe cortarse para dejar pasar otros enlaces. Crédito:Liu, Dehmamy y Barabási.
La estructura y funciones de muchas redes físicas, incluido el cerebro humano, el sistema vascular y otras redes biológicas, a menudo dependen de su diseño tridimensional y geométrico. Distinguir entre redes físicas con conexiones idénticas pero diseños geométricos diferentes, sin embargo, puede ser muy desafiante.
Investigadores de la Northeastern University han introducido recientemente una construcción teórica llamada isotopía de red que podría ayudar a los científicos a diferenciar entre redes físicas. La isotopía de red ofrece una herramienta de clasificación que describe clases de diseños de red 3-D que pueden transformarse entre sí sin cruces de enlaces.
"Nuestro proyecto comenzó como una curiosidad sobre los diseños de red, "Yanchen Liu, uno de los investigadores que realizó el estudio, dijo Phys.org. "Hay muchas redes impresas en 3D en nuestra oficina que se estudiaron en varios proyectos en el laboratorio. Al observar estas redes, nos preguntamos:si para una red determinada (cableado fijo de los enlaces) hay infinitas formas de colocar los nodos y enlaces en el espacio 3-D, ¿Cómo podemos saber si dos diseños de la misma red son iguales o diferentes? Es más, ¿Cómo debemos definir las similitudes entre los diseños de red y si dos diseños son diferentes, ¿Cómo debemos medir el nivel de diferencia entre ellos? "
Poco después de que comenzaran a realizar su investigación, Liu y sus colegas se dieron cuenta de que hay dos formas principales en las que los diseños geométricos de la red pueden diferir entre sí. El primero de ellos depende de la medida en que se estira el diseño de una red, mientras que el segundo resulta del llamado cruce de enlaces (es decir, enlaces que se cruzan entre sí).
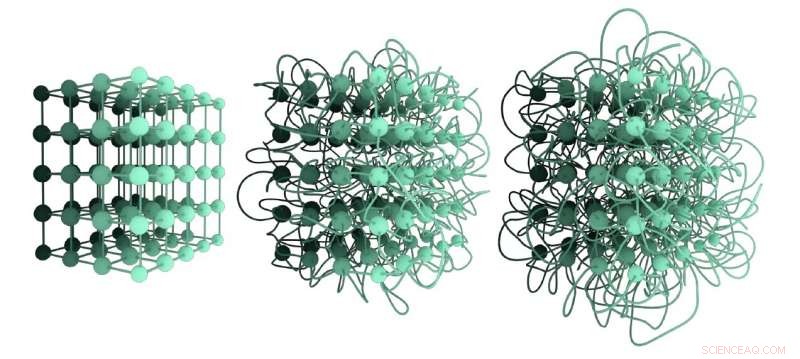
Tres incrustaciones no isotópicas diferentes de la misma red de celosía. La incrustación de la izquierda está desenredada; la incrustación en el medio está más enredada en comparación con la primera, y la tercera incrustación es la más enredada. Su nivel de enredo se puede cuantificar mediante el Número de enlace de gráfico. Crédito:Liu, Dehmamy y Barabási.
"El primer tipo de diferencia es trivial, pero el segundo tipo de diferencia es intrigante, "Explicó Liu." Se han estudiado preguntas similares en la teoría de nudos, que es un campo dedicado a los nudos formados por una o más curvas cerradas ".
La incrustación de una red física (es decir, layout) es esencialmente una descripción de cómo sus nodos y enlaces se unen en el espacio. En su papel Liu y sus colegas introdujeron un concepto llamado isotopía de incrustación de red que se puede utilizar para distinguir entre diferentes incrustaciones posibles de una red dada en el espacio 3-D.
"Si dos integraciones de red son isotópicas entre sí, significa que se pueden estirar entre sí sin tener que cortar ningún enlace para dejar pasar otros enlaces, "Dijo Liu." Por otro lado, si dos incrustaciones de red no son isotópicas entre sí, significa que nunca podrán transformarse continuamente entre sí sin cortar vínculos ".
La noción de isotopía de red, como lo define este equipo de investigadores, se puede utilizar para medir hasta qué punto se enredan las diferentes integraciones de red, una medida conocida como el número de vinculación del gráfico. Curiosamente, Liu y sus colegas encontraron que esta medida también se correlaciona con la energía elástica de un diseño.
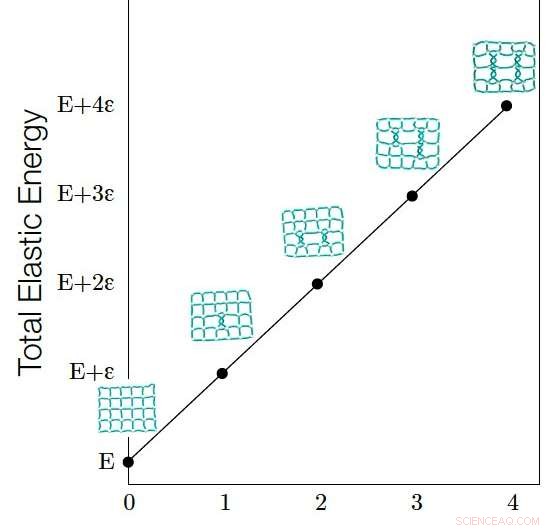
Se observa que la energía elástica (E) de la incrustación de una red está correlacionada linealmente con su Número de enlace de gráfico (G). La energía elástica de la incrustación de una red es proporcional a la longitud total de todos los enlaces. La relación lineal entre E y G se puede explicar por el hecho de que cada aumento en G estira los enlaces en la red incrustada, que a su vez aumenta E, y la cantidad de aumento de energía causado por cada enredo (cada enredo hace que G aumente en uno) se cuantifica y es una constante. Crédito:Liu, Dehmamy y Barabási.
Muchos sistemas físicos pueden describirse como redes, una parte significativa de las cuales son redes físicas. Los conceptos teóricos introducidos por los investigadores son herramientas eficaces para estudiar las propiedades y características geométricas de estos sistemas.
"Hay tres logros importantes en este documento, en mi opinión, "Dijo Liu." La primera es que definimos la isotopía de integración de red, que es una extensión de la isotopía de nudos desde la teoría de nudos hasta las incrustaciones de redes. La segunda es que inventamos el número de enlace de gráficos, una medida útil del nivel de enredo de las incrustaciones de red. Finalmente, descubrimos que el número de enlace gráfico de una inserción de red está correlacionado con la energía elástica de esa inserción de red ".
Liu y sus colegas utilizaron sus hallazgos para desarrollar un modelo estadístico que describe la formación de enredos en una red física. En el futuro, este modelo podría usarse para evaluar hasta qué punto se enreda el diseño tridimensional de un sistema físico.
En su artículo reciente, por ejemplo, los investigadores lo utilizaron para examinar el enredo de muchos sistemas físicos, incluido el cerebro del ratón. Como todos los constructos teóricos introducidos en este artículo se pueden aplicar a una amplia variedad de redes físicas, en última instancia, podrían apoyar la investigación en física centrándose en una amplia gama de temas.
"Ahora continuamos con el estudio de las redes físicas, "Dijo Liu." Actualmente, Estoy trabajando en una red física específica:la red del cerebro larvario de la mosca de la fruta, que es una red formada por neuronas incrustadas en el espacio 3-D. Estamos específicamente interesados en las conexiones entre la fisicalidad de esta red (su incrustación) y sus propiedades estructurales (cómo las neuronas están conectadas a través de cables neuronales) ".
© 2020 Science X Network