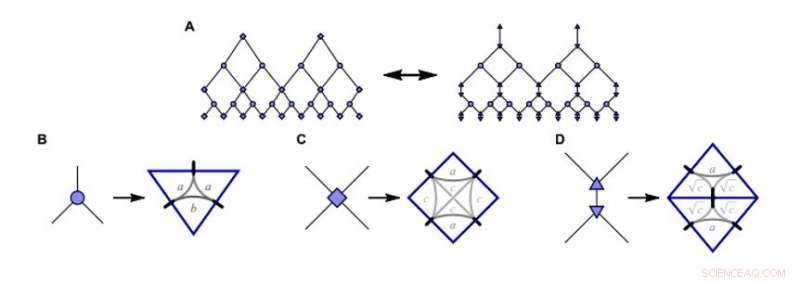
Construcción del modelo de juguete Matchgate MERA (simulación ansatz de renormalización de entrelazamiento multiescala; mMERA). R:La red de tensor estándar MERA (izquierda) en la configuración de la puerta de emparejamiento numérica del estudio es equivalente a B-D:Isometrías, desenredadores, y desenredadores triangulados (de izquierda a derecha) expresados como tensores de compuerta. Los parámetros libres a, B, c fijar los componentes de las matrices generadoras. Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
Las redes de tensores tienen un papel central en la física cuántica, ya que pueden proporcionar una aproximación eficiente a clases específicas de estados cuánticos. El lenguaje gráfico asociado también puede describir fácilmente y razonar pictóricamente sobre circuitos cuánticos, canales, protocolos y sistemas abiertos. En un estudio reciente, A. Jahn y un equipo de investigación en los departamentos de sistemas cuánticos complejos, Los materiales y la energía y las matemáticas y la informática en Alemania introdujeron un marco versátil y eficiente para estudiar las redes de tensores mediante la ampliación de las herramientas anteriores. Los investigadores utilizaron el mosaico masivo (técnica geométrica informática) en su trabajo para obtener datos críticos de alta precisión y establecieron un vínculo entre los códigos holográficos de corrección de errores cuánticos y las redes de tensores. Esperan que el trabajo estimule nuevas investigaciones de los modelos de redes de tensores para capturar correspondencias de límites de volumen. Los resultados ahora se publican en Avances de la ciencia .
La correspondencia AdS / CFT, que significa correspondencia anti-de Sitter / teoría de campo conforme, es una de las mayores áreas de investigación en teoría de cuerdas, y es un ejemplo en el contexto de dualidades de límite de volumen en el que existe una dualidad holográfica entre la gravedad en un espacio de volumen y un campo cuántico crítico en su límite. Esta correspondencia que relaciona dos teorías muy diferentes fue formulada originalmente por el físico Juan M. Maldacena en 1997, y se considera un resultado significativamente importante en la teoría de cuerdas en los últimos 20 años.
Una característica clave de estas dualidades es la relación entre la geometría masiva y las entropías de entrelazamiento de límites, que los físicos habían iluminado previamente usando la fórmula Ryu-Takayanagi. Dado que es importante comprender el entrelazamiento en el contexto de AdS / CFT, Los investigadores se dieron cuenta de la necesidad de las redes de tensores como marco ideal para construir modelos de juguetes holográficos, como la simulación ansatz de renormalización de entrelazamiento multiescala (MERA). Los físicos habían explorado previamente la comprensión de que la corrección de errores cuánticos podría facilitarse mediante una dualidad holográfica, que además se conectó con ideas de la teoría de la información cuántica. Aunque los investigadores construyeron con éxito varios modelos de redes de tensores para reproducir una variedad de aspectos en AdS / CFT, todavía carecían de una comprensión general de las características y los límites de la holografía de redes tensoriales. Los obstáculos específicos al proceso incluyen los espacios de parámetros potencialmente grandes de las redes de tensores y los considerables costos computacionales involucrados.
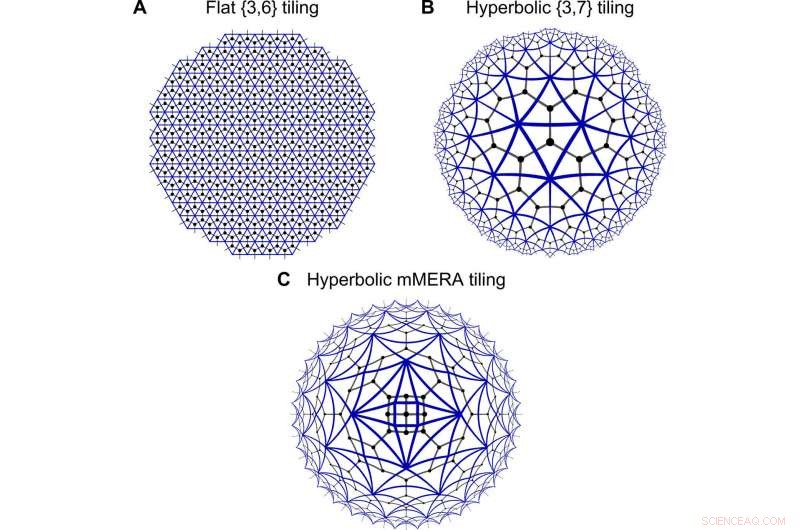
Geometrías de redes tensoriales. Discretizaciones de espacio plano (A) e hiperbólico (B y C) con un mosaico triangular (bordes azules), en el que está incrustada una red tensorial (celosía negra). En el formalismo de Matchgate, las aristas de unión entre triángulos corresponden a una integración sobre un par de números de Grassmann, análogo a la contracción de la red tensorial sobre índices. Mientras que (A) y (B) muestran mosaicos regulares, (C) presenta un mosaico no regular similar a MERA, que los científicos llamaron Matchgate MERA (mMERA). Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
En el presente trabajo, Jahn y col. superó los desafíos existentes mediante la aplicación de técnicas de contracción altamente eficientes desarrolladas por tensores de compuerta. Las técnicas versátiles permitieron al equipo de investigación estudiar de forma exhaustiva la interacción de la geometría y las correlaciones en las redes de tensores fermiónicos gaussianos mediante la incorporación de modelos de juguete de corrección de errores cuánticos. También incluyeron enfoques de redes de tensores anteriores como el modelo "MERA" dentro del presente trabajo, para resaltar las conexiones entre ellos. El equipo restringió el estudio a redes de tensores que no son unitarias y reales, asemejándose a una evolución euclidiana desde la masa hasta el límite. Jahn y col. proporcionó nuevos enfoques en el contexto de la renormalización de la red tensorial, para corroborar la capacidad de las redes de tensores para describir correspondencias de límites de volumen más allá de los modelos conocidos. El presente trabajo es preliminar y proporciona un punto de partida para estudios más sistemáticos sobre holografía en redes tensoriales.
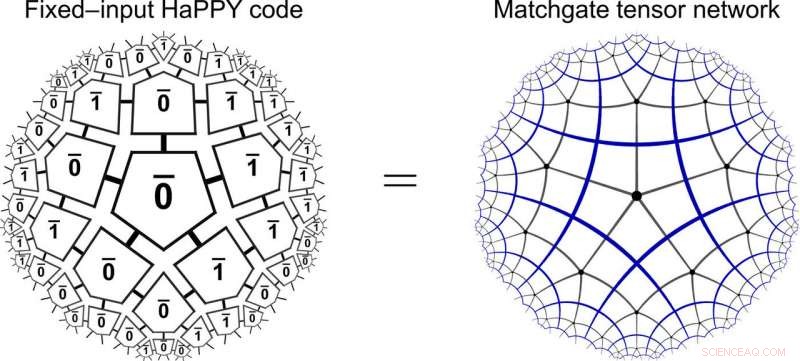
Equivalencia HaPPY / Matchgate. El código del pentágono holográfico del modelo HaPPY para la entrada masiva computacional fija (izquierda) es igual a una red de tensor Matchgate en un mosaico de pentágono hiperbólico (derecha). Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
Los científicos primero aplicaron su marco a la clase altamente simétrica de mosaicos a granel regulares para implementar el código de corrección de errores holográficos (código HaPPY) propuesto en otra parte. Después de eso, exploraron la versatilidad del marco para extenderlo hacia configuraciones más físicas. Primero usaron el modelo de juguete de código HaPPY para comprender la correspondencia de volumen / límite con el mosaico de pentágonos holográficos, donde cada mosaico del pentágono codificaba un qubit lógico tolerante a fallas. Brevemente, el equipo de investigación observó que la fijación de los grados generales de libertad a los estados de base computacional podría dar lugar a una red de tensor de matchgate. Demostraron que los estados de la base computacional eran gaussianos puros y concluyeron que para la entrada computacional fija en la mayor parte, el código del pentagrama holográfico podría producir un tensor de compuerta en el límite. Usando un símbolo de Schläfli {p, q} donde p =el número de bordes por polígono yq =el número de polígonos alrededor de cada esquina, especificaron la geometría hiperbólica del modelo HaPPY.
Después de Jahn et al. mostró su marco modelo para incluir el código pentágono holográfico construido a partir de estados estabilizadores de cinco qubit para entradas de volumen fijo. Demostraron que los estados de los límites se corresponden con el apareamiento masivo no local con partículas exóticas conocidas como fermiones de Majorana. El trabajo abrió así una vía para estudiar las propiedades estatales de un modelo holográfico en grandes tamaños. Los científicos calcularon además los correlacionadores de dos puntos y las entropías de entrelazamiento del sistema. Luego demostraron que los estados límite gaussianos críticos y con huecos podrían realizarse más allá de los modelos conocidos utilizando varios mosaicos masivos. En el presente trabajo reprodujeron las propiedades de escala promedio del modelo de juguete Ising CFT (teoría de campo conforme); modelo más simple posible en física teórica que permitió métodos de la teoría cuántica de campos euclidianos y el estudio de fenómenos críticos.
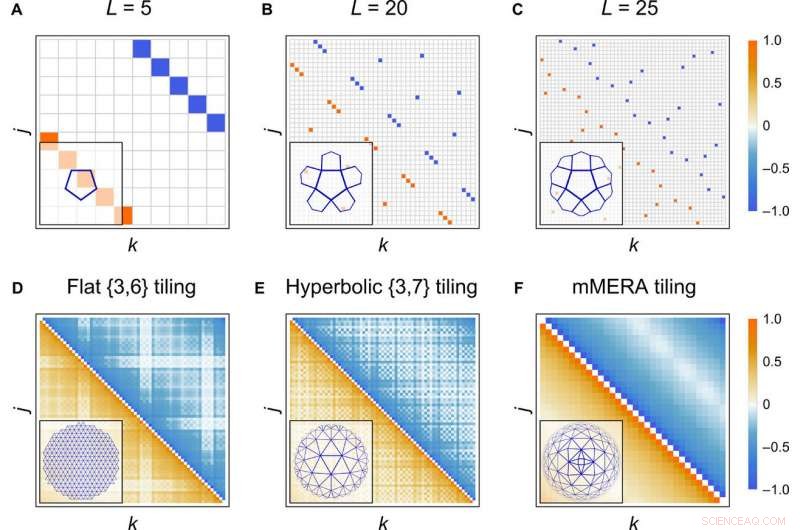
Correlaciones de estados de frontera. (A a C) Matriz de covarianza de Majorana Γ con entradas codificadas por colores para un estado límite de un hiperbólico {5, 4} mosaico del código HaPPY con entrada 0¯ fija en cada mosaico. El límite consta de 2L =10, 40, y 50 sitios de Majorana, respectivamente. (D a F) Matriz de correlación de campo 〈ψjψk - ψkψj〉 / 2 =(Γ2j, 2k − 1 + Γ2j − 1, 2k) / 4 para estados límite de {3, 6}, {3, 7}, y mosaico de mMERA en criticidad con L =63, 69, y 64 sitios limítrofes, respectivamente. Las entradas de la matriz se normalizan a la misma escala de colores. El mosaico correspondiente a cada matriz de correlación en (A) a (F) se muestra en la esquina inferior izquierda. Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
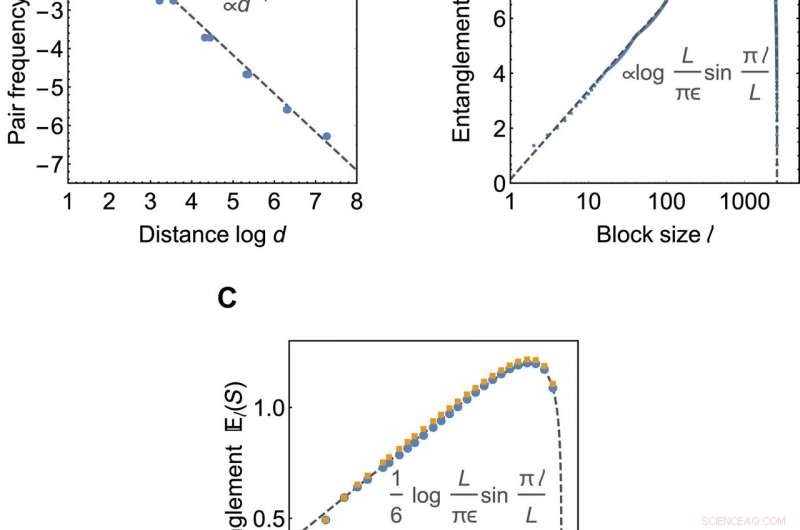
Correlaciones críticas y escalado de entrelazamientos. (A y B) Propiedades del estado límite del código HaPPY en 2605 sitios límite. (A) muestra las correlaciones promedio en la distancia límite d, calculada como la frecuencia relativa n de pares de Majorana. La línea gris discontinua muestra un ajuste numérico n (d) ~ 1 / d. (B) muestra la escala de la entropía de entrelazamiento promedio El (S) con el tamaño del subsistema l. La línea gris discontinua muestra un ajuste numérico usando (11). (C) El (S) para teselaciones regulares en los valores críticos a =0.580 para a {3, 6} mosaico (azul) y en a =0.609 para el {3, 7} mosaico (amarillo) con 348 sitios de límites cada uno. La línea gris discontinua muestra la solución c =1/2 CFT exacta. Crédito:Science Advances, doi:10.1126 / sciadv.aaw0092
Jahn y col. luego construyó una red de tensor de compuerta euclidiana basada en la geometría MERA desarrollada previamente y la nombró Matchgate MERA (mMERA). Esta invariancia de mosaico que expresaron como una triangulación (múltiples medidas para capturar una construcción), recuperó el Ising CFT con poco costo computacional. El proceso de optimización computacional en el estudio solo tomó unos minutos en una computadora de escritorio para una red con cientos de tensores.
De este modo, A. Jahn y sus colegas introdujeron un marco preliminar eficiente para estudiar las redes de tensores y propusieron estudios adicionales dentro del entorno gaussiano para centrarse en bultos con curvas positivas, modelos de dimensiones superiores y tensores aleatorios. Estudios adicionales más allá de Gaussianity podrían explorar las redes de tensor fermiónico interactuando por expansión de acoplamiento débil o bajo interacciones localmente restringidas. Las dos posibles extensiones sugeridas del marco presentado en el estudio solo requerirán un polinomio de escalado computacional al tamaño del sistema para evitar esfuerzos computacionales prohibitivos de los métodos generales para extraer la contracción del tensor.
© 2019 Science X Network