
¿Fueron las diferentes formas de enseñar el orden de las operaciones responsables de la confusión? Crédito:Shutterstock
Desde hace aproximadamente una década, los matemáticos y los educadores matemáticos han estado sopesando un debate particular arraigado en las matemáticas escolares que no muestra signos de disminuir.
El debate, cubierto por Slate, Popular Mechanics , El New York Times y muchos otros medios, se centra en una ecuación que se volvió tan "viral" que, finalmente, se agrupa con otros fenómenos que han "roto" o "dividido" Internet.
En el caso de que aún tenga que opinar, ahora sería un buen momento para ver cuál es su posición. Responda lo siguiente:
8÷2(2+2)=?
Si eres como la mayoría, tu respuesta fue 16 y te sorprende que alguien más pueda encontrar una respuesta diferente. A menos que seas como la mayoría de los demás y tu respuesta sea 1 y estés igualmente confundido acerca de verlo de otra manera. No temas, a continuación, explicaremos la respuesta definitiva a esta pregunta y por qué se debe prohibir la forma en que se escribe la ecuación.
Nuestro interés se despertó porque realizamos una investigación sobre las convenciones sobre el seguimiento del orden de las operaciones (una secuencia de pasos que se siguen cuando se enfrenta a una ecuación matemática) y estábamos un poco desconcertados con el motivo de todo este alboroto.
Claramente, la respuesta es...
¿Dos respuestas viables a un problema de matemáticas? Bueno, si hay algo que todos recordamos de la clase de matemáticas:¡eso no puede ser correcto!
Muchos temas surgieron de la plétora de artículos que explican cómo y por qué esta "ecuación" rompió Internet. Se discutió mucho la introducción de la expresión en las calculadoras, algunas de las cuales están programadas para respetar un orden particular de operaciones.
Otros, evadiendo un poco, sugieren que ambas respuestas son correctas (lo cual es ridículo).
El tema más dominante se centró simplemente en la implementación del orden de las operaciones según diferentes siglas. Algunos comentaristas dijeron que los malentendidos de la gente se atribuyeron a la interpretación incorrecta del acrónimo memorizado que se enseña en diferentes países para recordar el orden de las operaciones como PEMDAS, que a veces se usa en los Estados Unidos:PEMDAS se refiere a aplicar paréntesis, exponentes, multiplicación, división, suma y resta.
Una persona que siga este orden tendría 8 ÷ 2 (2 + 2) convertido en 8 ÷ 2 (4) gracias a comenzar con paréntesis. Luego, 8 ÷ 2 (4) se convierte en 8 ÷ 8 porque no hay exponentes, y "M" significa multiplicación, por lo que multiplican 2 por 4. Por último, de acuerdo con la "D" de división, obtienen 8 ÷ 8 =1.
Por el contrario, a los canadienses se les puede enseñar a recordar BEDMAS, que significa aplicar corchetes, exponentes, división, multiplicación, suma y resta. Alguien que siguiera este orden tendría 8 ÷ 2 (2 + 2) convertido en 8 ÷ 2 (4) gracias a comenzar con corchetes (igual que los paréntesis). Entonces, 8÷2(4) se convierte en 4(4) porque (no hay exponentes) y "D" significa división. Por último, según la "M" de la multiplicación, 4(4)=16.
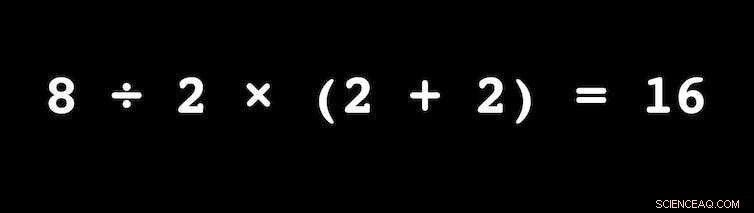
Si el problema se hubiera presentado correctamente como 8 ÷ 2 × (2 + 2) =?, no habría un debate acalorado. Crédito:Egan J. Chernoff, proporcionado por el autor
No omita el símbolo de multiplicación
Para nosotros, la expresión 8÷2(2+2) es sintácticamente incorrecta.
La clave del debate, sostenemos, es que se omite el símbolo de multiplicación antes de los paréntesis.
Tal omisión es una convención en álgebra. Por ejemplo, en álgebra escribimos 2x o 3a que significa 2 × x o 3 × a. Cuando se usan letras para variables o constantes, se omite el signo de multiplicación. Considere la famosa ecuación e=mc 2, lo que sugiere el cálculo de la energía como e=m×c 2.
Entonces, la verdadera razón por la que 8 ÷ 2 (2 + 2) rompió Internet proviene de la práctica de omitir el símbolo de multiplicación, que se trajo de manera inapropiada a la aritmética del álgebra.
Prioridad inapropiada
En otras palabras, si la expresión se hubiera "deletreado" correctamente, es decir, presentada como "8 ÷ 2 × (2 + 2) =? ", no se volvería viral, no habría dualidad, ni Internet roto, ni debates acalorados. ¡No es divertido!
En última instancia, la omisión del símbolo de multiplicación invita a una prioridad inapropiada a la multiplicación. Todos los comentaristas acordaron que agregar los términos entre corchetes o paréntesis era el primer paso apropiado. Pero surgió confusión dada la proximidad de 2 a (4) en relación con 8 en 8÷2(4).
Queremos que se sepa que escribir 2(4) para referirse a la multiplicación es inapropiado, pero entendemos que se hace todo el tiempo y en todas partes.
Buen símbolo para la multiplicación
Hay un símbolo muy bonito para la multiplicación, así que usémoslo:2 × 4. Si no te gusta, hay otros símbolos, como 2•4. Use cualquiera, a su gusto, pero no lo omita.
Como tal, para que conste, ¡el debate sobre uno contra 16 ya terminó! La respuesta es 16. Caso cerrado. Además, nunca debería haber habido realmente un debate en primer lugar.
Este artículo se vuelve a publicar de The Conversation bajo una licencia Creative Commons. Lea el artículo original. Un estudio explica cómo algunos cerebros más viejos se deterioran antes de que las personas se den cuenta
