
Cubo de Rubik en estado resuelto. Crédito:Mike Gonzalez (TheCoffee)
El cubo de Rubik ha sido uno de los rompecabezas favoritos del mundo durante 40 años. Se han ideado varios métodos diferentes para resolverlo, como se explica en innumerables libros. Los expertos "speedcubers" pueden resolverlo en cuestión de segundos.
Además de tales hazañas de asombrosa destreza, Hay muchas preguntas matemáticas fascinantes relacionadas con el cubo de Rubik. Un movimiento del cubo consiste en rotar una de las seis caras en 90, 180, o 270 grados. Un asombroso 43, 252, 003, 274, 489, 856, Se pueden obtener 000 estados posibles aplicando secuencias de movimientos al estado resuelto.
A pesar de esta complejidad, se demostró en 2010 que el cubo de Rubik siempre se puede resolver en 20 movimientos o menos, independientemente del estado inicial. Este número se conoce como "número de Dios, "ya que todos los métodos de solución conocidos utilizados por los seres humanos suelen utilizar significativamente más movimientos que este valor óptimo.
Pero, ¿qué pasa con la pregunta opuesta:cuántos movimientos se requieren para mezclar un cubo resuelto? A primera vista, suena como una pregunta mucho más fácil que calcular el número de Dios. Después de todo, a diferencia de resolver un cubo, revolver uno no requiere habilidad alguna.
Preguntas similares se han respondido con éxito para barajar cartas. Un ejemplo famoso es el estudio de 1990 del "riffle shuffle" realizado por los matemáticos Dave Bayer y Perci Diaconis. Una baraja de cartas se define como "mixta" si su orden es aleatorio, teniendo cada orden posible la misma probabilidad de aparecer. Bayer y Diaconis demostraron que son necesarias y suficientes siete combinaciones de riffle para mezclar aproximadamente una baraja estándar de naipes.
El año pasado, matemáticos publicaron un estudio similar del 15 rompecabezas, que consta de un cuadrado de 4x4 relleno con 15 tejas deslizantes y un espacio vacío.

Cubo de bolsillo en estado revuelto. Crédito:Mike Gonzalez (TheCoffee)
¿Qué significa que un cubo esté revuelto?
Una persona típica que intenta revolver un cubo de Rubik realizaría repetidamente movimientos aleatorios sobre él. La secuencia aleatoria de estados resultante es un caso especial de lo que los matemáticos llaman una cadena de Markov. La propiedad clave es que, dado el estado actual, la probabilidad de cuál será el próximo estado no depende de ninguno de los estados anteriores.
Aplicando la teoría de las cadenas de Markov a la codificación de cubos, se deduce que a medida que aumenta el número de movimientos aleatorios, la probabilidad de estar en cualquiera de los estados posibles se acerca cada vez más a 1/43, 252, 003, 274, 489, 856, 000. Los matemáticos llaman a esto una "distribución de probabilidad uniforme, "ya que cada estado posible ocurre con la misma probabilidad.
Después de cualquier número dado de movimientos aleatorios, el estado del cubo será aleatorio, pero su distribución de probabilidad no será exactamente uniforme; es más probable que ocurran algunos estados que otros.
Dejar d (t) describir en qué medida la distribución de probabilidad después t los movimientos aleatorios difieren de la distribución de probabilidad uniforme. A medida que el número de movimientos aleatorios ( t ) aumenta, El valor de d (t) va a disminuir. El cubo que se codifica corresponde a d (t) siendo pequeño.
Montecarlo de la cadena de Markov
En la teoría de las cadenas de Markov, esta disminución en d (t) se llama "mezclar". Además de barajar cartas y revolver acertijos, la teoría de la mezcla de cadenas de Markov también tiene aplicaciones prácticas muy serias. Una de las herramientas computacionales más importantes de la ciencia y la ingeniería modernas es el método Monte Carlo. Este método, como el famoso casino que le da nombre, se basa fundamentalmente en el azar. En esencia, intenta resolver aproximadamente problemas matemáticos difíciles utilizando múltiples conjeturas aleatorias.
En la práctica, Las cadenas de Markov se utilizan a menudo para producir estos estados aleatorios. Para comprender la precisión de estos métodos Monte Carlo de cadena de Markov, la tarea clave es estimar qué tan rápido d (t) disminuye a medida que t aumenta.
El cubo de bolsillo
Estudiar el problema de la codificación para el cubo de Rubik estándar de 3x3x3 es actualmente un desafío fascinante sin resolver. Sin embargo, se vuelve bastante manejable si prestamos atención a una versión 2x2x2 más pequeña, llamado el cubo de bolsillo.
En este cubo las piezas del borde y del centro están ausentes y solo quedan las piezas de las esquinas. El cubo de bolsillo tiene solo 3, 674, 160 estados posibles, y su número de Dios es solo 11.
En el siguiente gráfico, trazamos d (t) para el cubo de bolsillo. Después de 11 movimientos, d (t) sigue siendo muy grande, en 0,695. El primer valor de t que produce un d (t) valor por debajo de 0,25 (a menudo llamado "el tiempo de mezcla" en la teoría de la cadena de Markov) es 19. Después de 25 movimientos d (t) es 0,092; después de 50 movimientos es 0,0012; y después de 100 movimientos es 0.00000017.
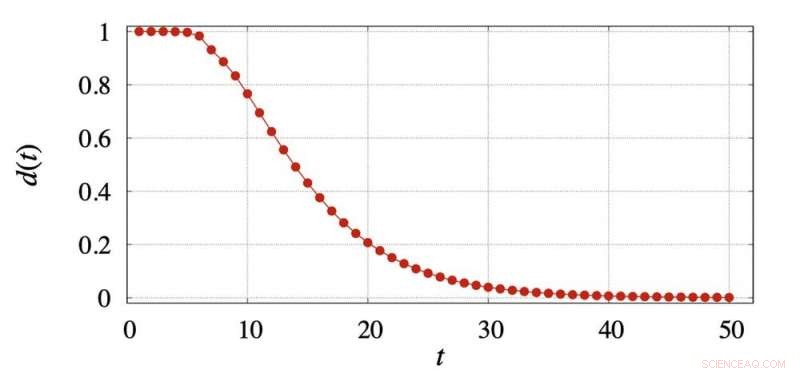
Distancia de la distribución del cubo de bolsillo del uniforme después de que t se mueve. Crédito:Eric Zhou
Entonces, ¿cuántos movimientos deberías usar para revolver completamente un cubo de bolsillo? La respuesta depende de lo pequeño que le gustaría d (t) ser. Sin embargo, ciertamente es cierto que el número de movimientos de Dios es insuficiente. Como mínimo, no se deben usar menos de 19 movimientos. Más detalles, incluyendo código para calcular d (t) , están disponibles aquí.
Y por supuesto, una vez que hayas revuelto tu cubo, todo lo que queda por hacer es resolverlo de nuevo.
Este artículo se vuelve a publicar de The Conversation con una licencia de Creative Commons. Lea el artículo original. 